What are the Magical Clocks for?

At Re:Invent last week, AWS announced DSQL, their new serverless SQL database. As a fan of distributed SQL databases I have been enjoying reading about the various architectural decisions in Marc Brooker’s blog.
One thing I thought was fun to see was the first real retread of the Spanner atomic clocks trick since…Spanner? So I thought this would be a good opportunity to talk about what the point of the atomic (hence: magic) clocks even is. If you're not familiar, Spanner was in part notable for its use of extremely accurate clocks in datacenters to provide consistency. Prior, most people had accepted that we had to make do with Lamport Time.
The trick winds up being colocated with consensus, but only really because both things are associated with “strong consistency” and “distributed system,” and the idea behind using a very accurate clock for consistency works just fine even in the absence of Paxos- or Raft-like protocols.
To the best of my knowledge, despite being a concept in the realm of consistency, the "clock trick" is only really necessary in a distributed transactional database, which is why we've only really seen it in Spanner and now DSQL, and it has an important connection to multi-version concurrency control (MVCC). Of course, as the existence of a number of open-source Spannerlikes that don't have the ability to rely on atomic clocks demonstrate, the clocks aren't necessary for serializable transactions.
So, then what is this whole idea for? As Marc says, it’s about strong consistency. People sometimes use “consistency” to refer to any kind of correctness condition for databases, as a blanket term that includes, for example, isolation. I don’t particularly like this: I think distributed systems correctness is “consistency” and transaction correctness is ACID (whose "C" also stands for "consistency," but a different meaning of "consistency." It's fine. Don't worry about it).
First, let's discuss MVCC. MVCC is a model where a value can take on multiple different "versions" over time. To read "at a timestamp" is to observe the value as it existed at that timestamp. To write "at a timestamp" is to install a new version so that any reads that come after it (but before the next write) will see that version. If you accept that all the keys have comparable timelines, you can use this to read a snapshot of the entire database as of a particular time without having to worry about your data getting invalidated:
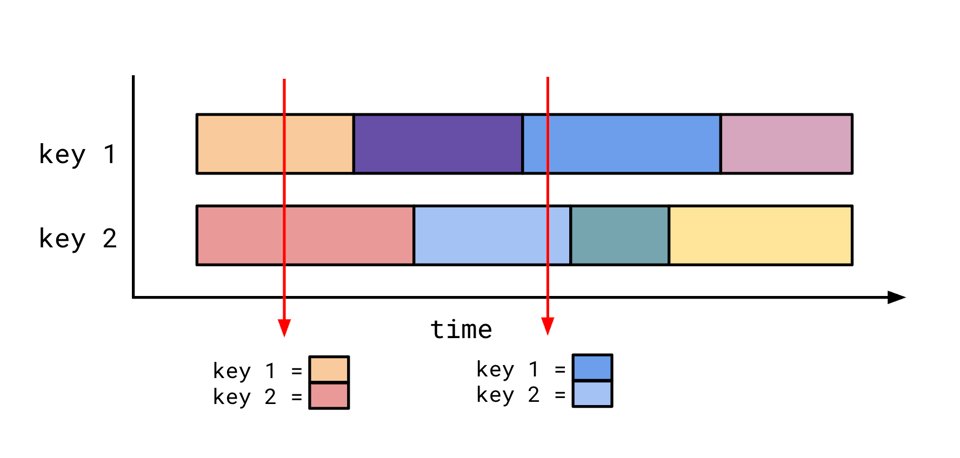
In this diagram, the two red arrows each denote a reader. They pick a timestamp, which is a vertical slice through the keyspace, and perform all of their reads at that timestamp. This makes providing a consistent read snapshot to a transaction easy: pick a timestamp, and perform all your reads as of that timestamp.
There's some subtlety hiding in "pick a timestamp" that we need to unpack.
Recall that linearizability very informally means "causality is preserved." If action A causes action B, then action B should see the events of action A.
Imagine for a second that we have no rules about how we pick timestamps. Then the following can happen:
Person 0 gets assigned timestamp 0 and writes x = 4
Person 1 gets assigned timestamp 1000 and writes x = 5
Person 1 sends a message to Person 2 and tells them to look up x
Person 2 gets assigned timestamp 500 and reads x = 4
This is no good: person 2's read was directly caused by person 1's write, but person 2 didn't see the effects of person 1's behaviour.
Luckily, if you care to, it's "easy" to provide monotonic timestamps in most situations like this:
- if you have a single-node database, the database can ensure that its timestamp assignment is monotonic with an atomic counter.
- If you have a distributed non-transactional database, you can store timestamp information next to each key, so that anyone who touches a particular key can get a monotonic "next timestamp."
The problem, then, can only be in distributed, multi-key read situations. Here's an example:
Person 0 gets assigned timestamp 0 and writes x = 0, y = 0
Person 1 gets assigned timestamp 1000 and writes x = 10
Person 1 sends a message to Person 2 and tells them to write y
Person 2 gets assigned timestamp 500 and writes y = 10
Person 3 gets assigned timestamp 750 and reads x = 0, y = 10
Now, following the causal chain of events, there should be the following valid states:
x = 0, y = 0
x = 10, y = 0
x = 10, y = 10
However, person 3 observes a state that was none of these, they saw x = 0, y = 10.
In a system that uses logical clocks, person 1, when they communicate to person 2, will give them a timestamp, which will guarantee that person 2 doesn't read earlier than person 1 did. And if all the lines of communication are internal to the system, that's sufficient, since all the causality is tracked in these timestamps. The problems arise if person 1 communicates to person 2 outside of the system, via a back channel. The guarantee that this doesn't happen is for this reason sometimes called external consistency.
The classical way to resolve this problem is to have the owners of x and y coordinate to ensure that any timestamp assignment for a transactions touching both of them to remain monotonic. They could talk to each other and bump of the timestamps of x and y to be comparable. But this requires coordination. There's another way: with the magic clocks.
Now, the magic clocks are not perfect, they're not accurate to like, Planck time, or something. But they come with a guarantee that no two of them disagree by more than some bound. That is, when a server observes the time to be t, it knows that no other server will observe the time to be earlier than, say, t-100. The clocks of all the participants in the system are racing along a timeline, but there's a fixed-size window that they all fall within.
This guarantee can be used to prevent the situation we described above. The guarantee we want is that once an operation finishes, no other operation will be ordered before it ever again. Once I assign timestamp t, I don't want anyone to ever assign a timestamp before t. How do I do that?
I wait for t+100 before I acknowledge the operation. As of t+100, nobody else will ever assign a timestamp before t+100-100 = t, which is exactly the requirement I have.
This highlights, I think, one of the benefits of increasingly accurate clocks: the more precise the bounds you provide are, the less you have to wait out the possible skew, and the better latency you can provide.
Links
Thanks Shachaf and Alex for providing some feedback!
Add a comment: