Trampolines for SQL

It is CIDR time and that means there is a lot of out-there papers in the world of databases to look at. If you are not familiar, CIDR is the Conference on Innovative Data Systems Research, which basically means it's a conference for academics to present their slightly goofier, slightly more esoteric, slightly more half-baked ideas. Sadly if you are a database person who is not that interested in AI, it is plagued with many of the problems that other database conferences have: which is that a solid half of all of the papers are about either applying AI to databases or databases to AI. Despite that, there are still a few nugs out there for the database-non-AI sickos.

We're going to talk about one paper in particular today but we will start with a detour.

Euclid’s Algorithm is an algorithm for computing the greatest common divisor of two numbers x and y. It works like this: you write down x and y in boxes, then you do the following:

• if y is 0, stop and output x as the GCD.
• otherwise, write x mod y in the y box, y in the x box, and start over.

Structurally, this algorithm looks like:

• write down some fixed number of values in boxes,
• examine those values,
• based on them, either output a result, or change some of the values in the boxes and start over.

This kind of computation is called iteration and there are two popular ways of expressing it: loops and tail recursion.

Implementing it with loops looks like this:

function gcd(x, y) {
    while (y !== 0 ) {
        let t = y;
        y = x % y;
        x = t;
    }
    return x;
}

and implementing it with tail recursion looks like this:

function recGcd(x, y) {
    if (y === 0) {
        return x;
    } else {
        return recGcd(y, x % y);
    }
}

Since loops and tail recursion both express exactly this kind of algorithm, they’re equivalent: everything you can express with a loop you can equivalently express with tail recursion, and vice versa.

In some languages, we might run into problems with tail recursion. Let’s compute the sum of two numbers in a weird way:

function sum(n, m) {
    while (m > 0) {
        n = n + 1;
        m = m - 1;
    }
    return n;
}

console.log(sum(100000000, 10)) // => 100000010

Implementing this with recursion we might run into a problem:

function recSum(n, m) {
    if (n === 0) {
        return m;
    } else {
        return recSum(n - 1, m + 1);
    }
}

console.log(recSum(100000000, 10))

/Users/justin/dev/trampoline/index.js:30
        if (n === 0) {
        ^

RangeError: Maximum call stack size exceeded
    at recSum (/Users/justin/dev/trampoline/index.js:30:2)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)
    at recSum (/Users/justin/dev/trampoline/index.js:33:10)

Oops, we blew out our stack.

Some languages replace a call in a tail position with a jump so that we don't get a stack overflow. Many—most—don't. One of the old classic tricks for implementing this sort of thing in a way that still resembles recursion is a trampoline. It looks like this:

function trampoline(f) {
    while (typeof f === 'function') {
        f = f()
    }
    return f
}

function g(x, y) {
    if (y === 0) {
        return x
    } else {
        return () => g(y, x % y);
    }
}

function h(n, m) {
    if (n === 0) {
        return m
    } else {
        return () => h(n - 1, m + 1);
    }
}

console.log(trampoline(g(42, 56)))
console.log(trampoline(h(100000000, 10)))

Each time we want to do a recursive call, our function either returns an actual result, or another function which should be called to continue the computation. Since we return back to the trampoline function after each call, we never truly recurse, and our stack never gets larger than one extra frame. This is why it's a "trampoline:" we bounce up and down our stack with each recursive call.

Trampolines-Style Queries for SQL is a CIDR paper from TUM that uses this same basic idea as a way to generalize and improve upon the classic WITH RECURSIVE style queries (that frankly, suck, and have needed improvement for a while). I'll be honest: when I first looked at the paper I thought it was a joke. I mean, look at this:

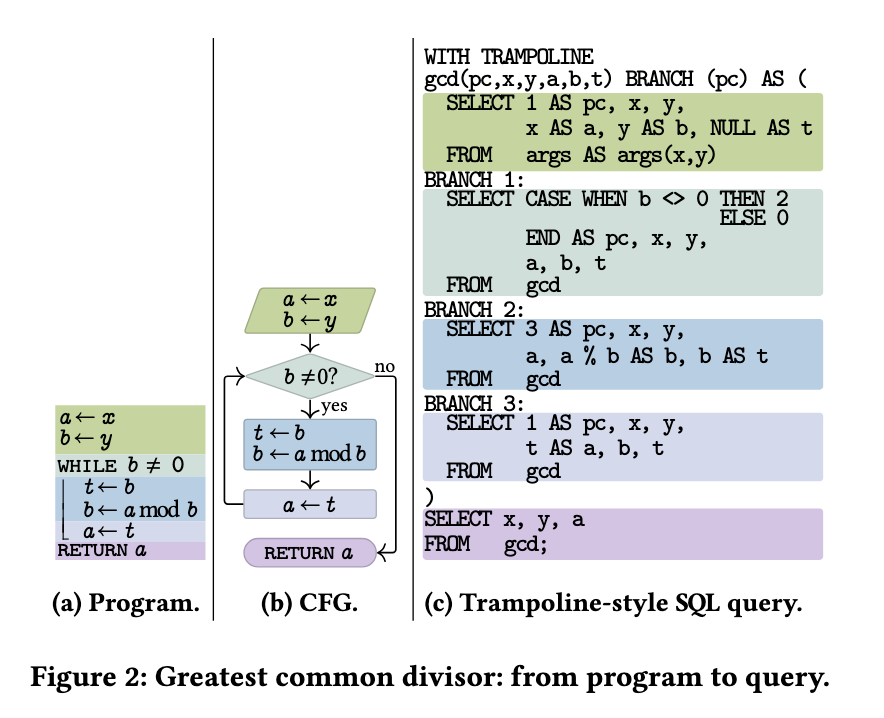
But after reading it in more detail and realizing that they're serious, I've changed my mind: I think it actually is a pretty nice model.

It is, at its heart, the same idea as the trampolines we talked about before, though serving a different purpose. It's not to avoid stack blowouts, but to reify the idea that we can represent further computations as data.

Semantically, each branch evaluates to zero or more rows. Any rows that get returned from a branch are fed back into it, until we have no more rows to issue a computation with, at which point it's done. In that way, it very much resembles a classic kind of fixpoint computation, which keeps feeding data back into a function until the total set stops changing.

They provide a bunch of examples, the one that excites me most is their observation that you can (statically, only looking at the schema) determine the set of rows that have to be deleted as part of an ON DELETE CASCADE foreign-key relationship, which was annoying when I had to do it myself:

I think this is a cool idea, and even if its not something worth exposing to users, it does make sense to me as a tool that would be really nice to have as a compilation target.