The Geometry of SQL

Today I want to talk about a way to think about some relational algebra operations.

First, let's start with this relation:

This is just a handful of games that appeared on a handful of systems, but let's pretend this was a complete list of games.

One way to visualize this data is as a set of points in a 3-dimensional space (the third dimension here is the value of copies_sold):

This might not seem like a super useful way to think about this data, and it's...well, sort of not, for most things you'd want to interact with it for. It does, however, provide some interesting interpretations of various relational algebra operations.

Projection

SELECT title, copies_sold FROM video_games

Imagine looking at the above picture as a being who lived in a universe with no platform dimension. What a crazy world that would be. If you did that, the image would look something like this, instead.

One way to think about this is that it's the shadow that the first picture casts onto a world with only the columns title and copies_sold. This is why this operation is called "projection" in the first place, because like vector projection (image from Wikipedia), where we take the shadow one vector casts onto another,

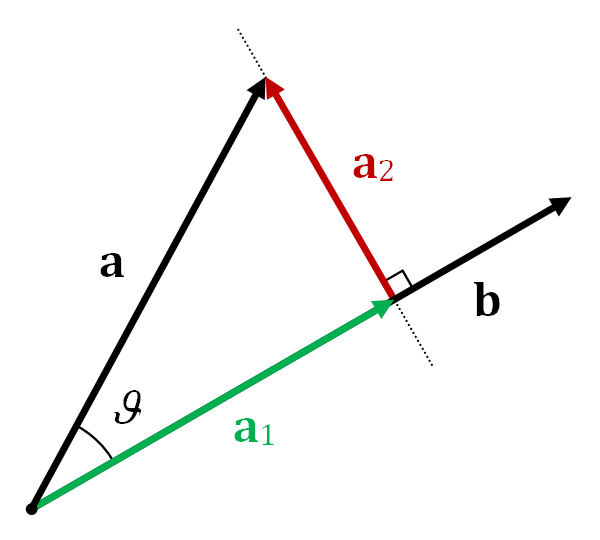
we're taking the image of some higher-dimensional object as viewed from some lower-dimensional space.

Aggregation

SELECT platform, sum(copies_sold) AS total_copies_sold FROM video_games GROUP BY platform

Again imagine looking at the first picture, but this time as a being with only a platform dimension. You might imagine this as like, standing underneath the first picture and looking up. This time, we see something interesting: some of the points obscure other points. This could have been true in the first case as well, it just happened to not be for this dataset.

One point of articulation that we have here is what it means when there are points obscuring each other: how do we resolve that? With the projection example, we just say, whatever. In SQL this would mean we'd emit duplicate rows. In a relational language that didn't permit duplicated rows in a relation, it would just ignore any repetitions. Another option we have is to combine all the points in some way, like pieces of glass being layered over each other. In the query above, we combine them with sum.

The picture looks something like this:

In this way we can compute the total sales numbers across various platforms.

Joins

It's also possible to interpret joins in this context, though it's a little trickier to visualize.

Given these two relations, R:

and S:

We can imagine each of these as, as before, sets of points in a two-dimensional space.

We're going to align their b axes:

Imagine in a 3-D space, which I don't have the capability to make a good diagram for, where the three spatial axes are a, b, and c, and where the two diagrams share a b axis, and have orthogonal a and c axes. Then extruding the points of each relation and taking their intersection, the result is the join, which casts a shadow contained in each input relation.

This model is sometimes used in the world of Worst-Case Optimal Joins to think about bounds on join sizes. This is not a proof, but if you imagine a cube in a three-dimensional space, that cube casts a square shadow on each of the planes that abut it. So if each square is size n, that means the cube can be at most n^1.5, which is the well-known result of the triangle join bound.

* Editor's note: Sin and Punishment, now there is a good game. You fire that bad boy up on an emulator and you'll have yourself a good ol' time.