Physical Properties #1

I wanna talk about relational algebra. Specifically, the things relational algebra is not concerned with, but obviously matter. Things like: ordering of a result set, distribution of data, that sort of thing. Because even though relational algebra, typically, does not distinguish between these two:

1
2
2
2
3

and

2
1
2
3
2

I can. And if I know my data is going to look like the left side, that it's sorted, I can do certain things more effectively. We can dedupe it without O(n) memory, or we can merge join it with another relation, or we can aggregate it without an index.

Lots of things are just better when our relations are sorted, despite the fact that our query languages don't typically have this notion.

The way this kind of thing is typically handled is via physical properties. These are, unhelpfully, in my opinion, usually defined as "properties of a result set that are not part of the query language," or something. An equivalent definition that I think is a little bit more helpful is that a physical property is one that can be enforced. It's a property for which we can insert an operator into our tree to make sure it has it. We can insert a sort to make sure a result set is ordered. We can insert a shuffle to make sure a result set is partitioned. We can do this precisely because of what we said before, that the query language is "blind" to these aspects of a result set, so to the logical computation, such operators are no-ops.

The classic physical property is, of course, ordering. So that's what we'll talk about.

The setup for thinking about physical properties is that a result set, which is a physical set of rows that might be processed during query execution, can satisfy, or not, a given physical property.

Then, a query plan satisfies a physical property if every result set it could produce satisfies that physical property.

Finally, a physical property A is as strong as as physical property B if every result set that satisfies A also satisfies B. This induces a partial order on physical properties, and we can write A >= B.

That's all a bit abstract so let's come back to ordering as an example. An ordering is a list of columns. A result set satisfies an ordering if it is sorted when comparing those columns lexicographically.

This result set:

 a | b
---+---
 1 | 3
 2 | 1
 2 | 2

Satisfies <a>, but not <b>. It also satisfies <a, b>, since on the rows where a agrees, it's ordered on b. In fact, any result set that satisfies <a, b> also satisfies <a>. This means that <a, b> is as strong as <a>. The converse isn't true: there are result sets that satisfy <a> and not <a, b>, so <a, b> is actually stronger than <a>.

The general rule is that an ordering is as strong as, and in most cases stronger, than all of its prefixes. I'll spare you a proof of this fact, but it's not too hard to show (and should make intuitive sense, with some thought).

If you were to draw what the ordering partial order looks like, it's something like a rooted tree, where each edge is labelled with a column. The set of orderings on three columns would look something like this:

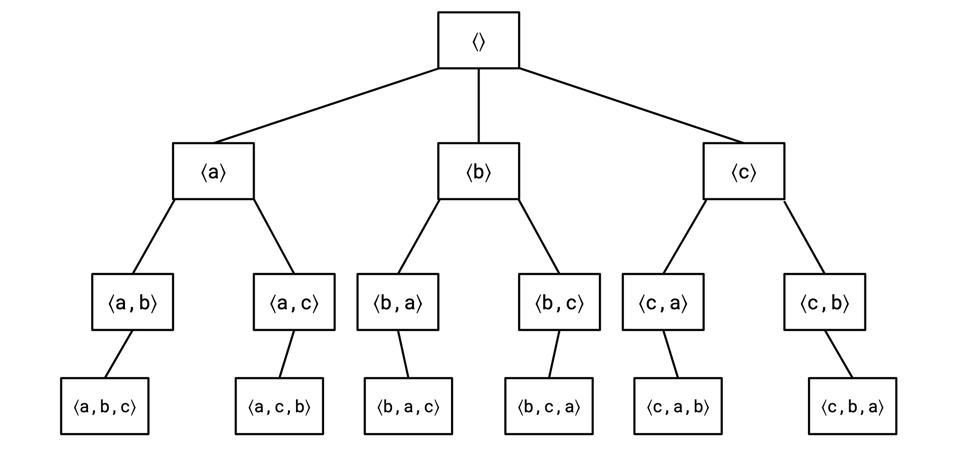
And one ordering is as strong as another if it passes through it on its way to the root.

There is more on this topic that I want to cover, but it's going to take a couple weeks. My hope is that in getting into this topic, we will eventually pay off a promise made in the very first issue of this newsletter.