Parsing is Search

Something I didn't appreciate for a while (despite the term backtracking being prevalent in both cases) was the extent to which parsing is a search problem. I don't really mean like, actual parsing you'd do on a day-to-day basis for a normal programming language. In those cases you'd typically try to design your grammar to be as easy to parse as possible so you don't need to think about it so much (though the exact way you tend to make it "easy" made more sense to me under the model we're going to talk about here). I mean "you are presented with an arbitrary grammar to parse."
Imagine a simplified case of regular expressions where we can just mark characters as optional.
So:
ab?c
matches "abc" or "ac."
Let's model this in code. Maybe we can model it by having objects which can consume some prefix of a string off of an input. A reasonable-looking way to implement this might look like this:
// A parser is a function which accepts a string and returns either:
// * the unparsed suffix of the string, if parsing was successful, or
// * false, if parsing was unsuccessful.
// Parse exactly the given string and return what's left.
const Const = str => input => {
if (input.startsWith(str)) {
return input.slice(str.length);
}
return false;
};
// Each parser in sequence must succeed.
const Concat = (...parsers) => input => {
for (let p of parsers) {
input = p(input);
if (input === false) {
return false;
}
}
return input;
};
// Parser is allowed to either succeed or fail. Question mark operator.
const Optional = parser => input => {
let rest = parser(input);
// If the parser fails, just say it didn't consume any input.
if (rest === false) {
return input;
}
return rest;
};
const matches = (parser, str) => {
return parser(str) === "";
};
console.log(matches(Const("abc"), "abc")); // => true
console.log(matches(Const("abc"), "abcd")); // => false
console.log(matches(Const("abc"), "ab")); // => false
console.log(
matches(
Concat(
Const("abc"),
Optional(Const("def")),
Const("ghi"),
),
"abcdefghi",
),
); // => true
console.log(
matches(
Concat(
Const("abc"),
Optional(Const("def")),
Const("ghi"),
),
"abcghi",
),
); // => true
This model is compelling and it is wrong. It fails to handle expressions like this:
let parser = Concat(
Const("abc"),
Optional(Const("def")),
Const("def"),
);
console.log(matches(parser, "abcdefdef")); // => true
console.log(matches(parser, "abcdef")); // => false, but should be true!
Our model isn't smart enough to handle the case where our optional parser can parse its input, but for a parse to be successful, it must fail. It doesn't know this ahead of time, it might have to indeed parse the def it sees. This is why this is a search problem: we're presented with two options: Optional can either parse the def it sees, or it cannot, and we don't know which is correct ahead of time.
Since Optional(Const("def")) must be able to either take, or not take, def, our parsing will look something like a tree. In this diagram, at each node, the top is the regular expression to be matched, and the bottom is the string to be matched:
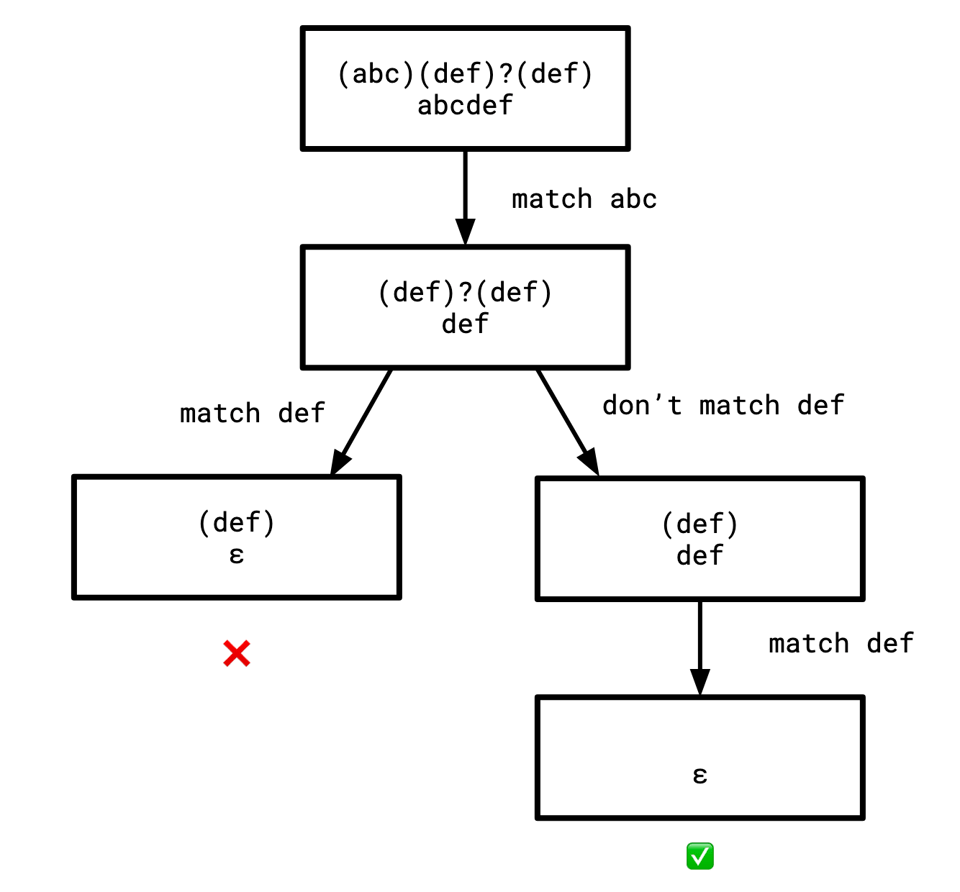
It should be noted that this kind of suggests a model where the only thing we're allowed to look at at any point in time is the leftmost elements of a string. This is typical in parsing situations, we usually assume we're slurping up characters from the left-side (although there are a handful of parsing algorithms that don't use this model).
This suggests that the way to fix our code above is to allow it to perform this kind of backtracking, and once it does our matching problem becomes just a tree search.
This is also true of dealing context-free grammars. I think parsing a language according to a context-free grammar is best understood by thinking of it as reversing the process of generating a string via a context free grammar.
Imagine the following grammar:
S -> hello, my name is N!
S -> hello, my name is N, what's yours?
S -> hello, i'm N.
N -> john
N -> jeff
N -> sam
It's easy to write a program that generates a string according to this grammar:
function N() {
let pick = Math.floor(Math.random()*3);
if (pick === 0) {
return "john";
} else if (pick === 1) {
return "jeff";
} else if (pick === 2) {
return "sam";
}
}
function S() {
let pick = Math.floor(Math.random()*3);
if (pick === 0) {
return `hello, my name is ${N()}!`;
} else if (pick === 1) {
return `hello, my name is ${N()}, what's yours?`;
} else if (pick === 2) {
return `hello, i'm ${N()}.`;
}
}
console.log(S());
console.log(S());
console.log(S());
console.log(S());
hello, my name is sam, what's yours?
hello, my name is john!
hello, my name is jeff!
hello, i'm sam.
A top-down parser is one that takes a string that was produced via application of these kinds of rules (where S is our starting symbol), and, starting from a starting symbol, tries to figure out the sequence of applications that could lead to deriving the string in question by trying to derive the start symbol. This is opposed to a bottom-up parser that folds up symbols as it reads them and hopefully winds up with the start symbol at the end of it all.
In our top-down world, starting from S, we have three alternatives corresponding to the three rules that have S as the left-hand side.
Aside: the fact that there is only ever a single nonterminal on the LHS of a rule is what makes this grammar "context-free" as opposed to "context-sentitive," there's no "context" around a nonterminal.
When a top-down parser is given the string hello, my name is sam, what's yours, it can't tell from looking at just the first character, h, whether it should follow the first rule, S -> hello, my name is N!, or the second rule, S -> hello, my name is N, what's yours?. We again have a choice to make: which rule do we guess was used to generate this string? Where this becomes a search problem is that we can just guess, and if it winds up not working, we can backtrack and guess again. In this case we won't know our guess was wrong until after we've parsed N, but that's okay. A tree for this search might look something like this:
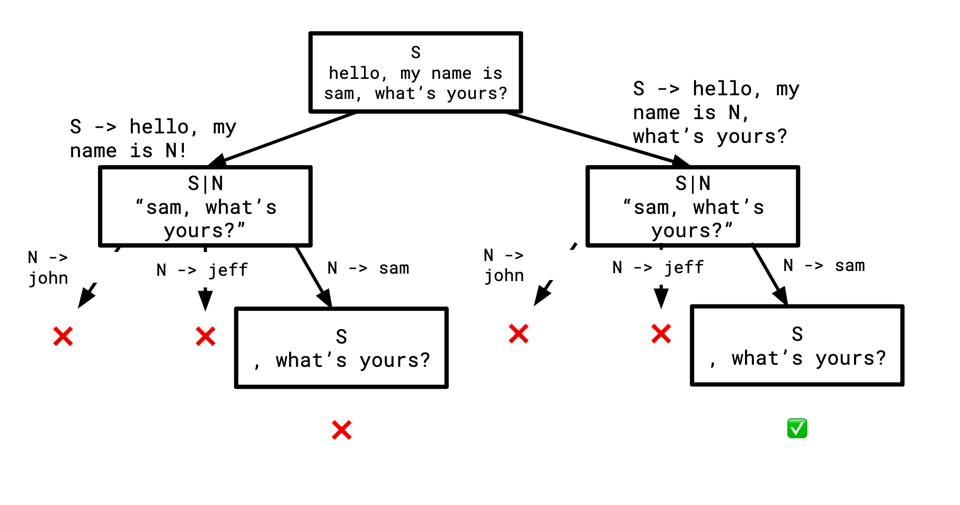
Of course, this is a simple such tree, but it could be deeper and you could have to backtrack further. I wrote about a more complex example that requires this kind of backtracking in SQL's Grammar Ambiguity (in hindsight I regret using the word "ambiguity" there since that has a technical meaning which is not this).
Consider instead a grammar that looks like this:
S -> ab
S -> B
S -> ca
B -> ba
Now, looking at the first character we see, we actually can determine which rule we should choose, since the map from "rule" to "first character that can be derived from that rule" is injective:
a: use S -> ab
b: use S -> B
c: use S -> ca
When grammars have this nice property where we never have to backtrack like that we call them LL(1). If you've ever written a recursive descent parser you might notice that for some languages you only have to peek one character ahead to know what function to call next: this is the property that makes that work.
If there are multiple paths through the search tree that result in a valid parse, then a grammar is ambiguous. Fun fact: there are context-free languages that have only ambiguous grammars. They (and much more) are discussed in some more depth in the wonderful book "Parsing Techniques - A Practical Guide:"

This is part of the thing that people like about PEGs, which is that they sort of eschew search by having any choices to be made have a distinct order to them, so there is always a defined order to try all the alternatives in and there is no chance of any ambiguity.
This perspective (parsing is search) was revelatory to me because the structure of various parsers has always seemed very mysterious. I always just said "well write a recursive-descent parser and hope it works out," and it wasn't until the whole thing was framed as a search problem did it all come together what is actually happening there, and how basically every other parsing algorithm I've ever encountered works by guiding this search in some way.
Add a comment: