Not all Graphs are Trees

It's pretty easy to imagine how to represent relational algebra expressions as a tree—they are already structurally rooted trees where each operator has its inputs as children.

Even in a language like Rust, which has not yet implemented mutable aliasing (an oft-requested feature stuck at the RFC stage) we can implement this easily:

enum RelExpr {
    Table(String),
    Join(ScalarExpr, Box<RelExpr>, Box<RelExpr>),
    Filter(ScalarExpr, Box<RelExpr>),
    Project(HashSet<ColumnId>, Box<RelExpr>),
}
...
let query = RelExpr::Join(
    q,
    Box::new(
        RelExpr::Filter(
            p,
            Box::new(RelExpr::Table("R".into()))
        )
    ),
    Box::new(
        RelExpr::Project(
            c,
            Box::new(
                RelExpr::Table("S".into())
            ),
        ),
    ),
);

Things get hairier if we want to introduce some kind of non-tree structure into our query, like some kind of self-join:

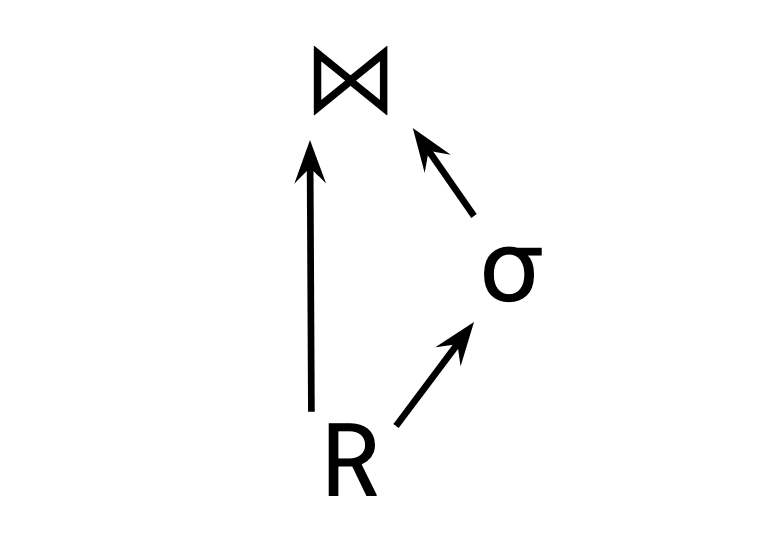
This structure permits neither an easy textual representation nor an easy Rust representation (interestingly, these are sort of the same thing).

There's a couple of ways to resolve this problem.

Inlining

The first is inlining. Which is to simply duplicate the expression we want to reference twice.

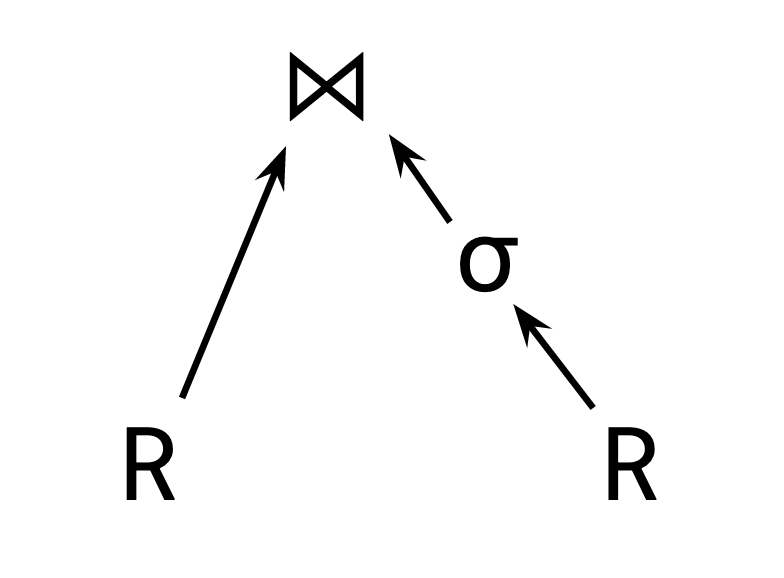
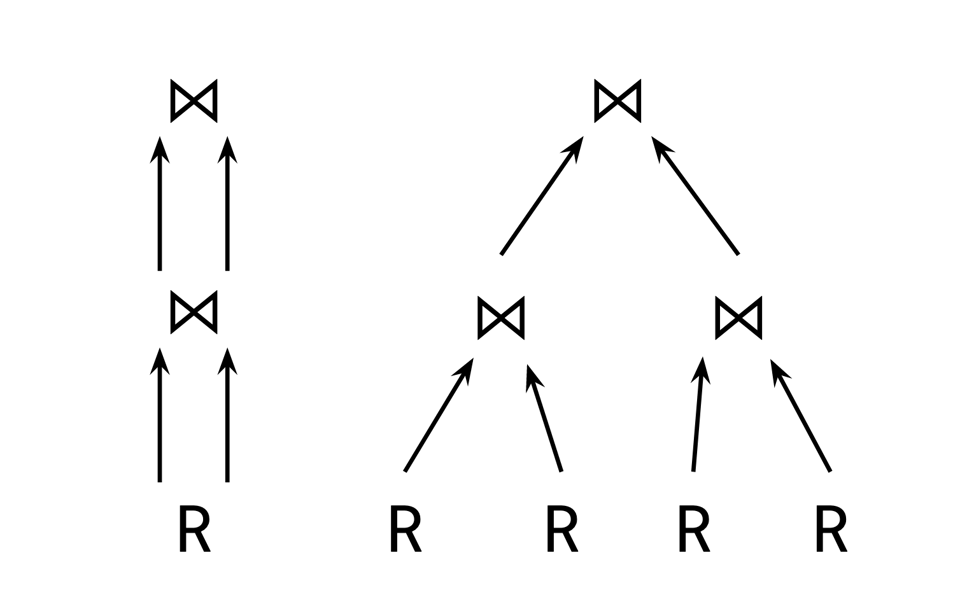
This works! But is non-ideal when the expression being referenced is complex, since we'll have a lot of duplicated expressions, and, if we recompute them each time, a lot of duplicated work. Even worse is that multiple nested occurrences of multiple references can result in an exponential blowup in the size of the tree:

Let Binding

The other option to resolve this is to use some kind of let-binding. This is directly supported in SQL as a WITH clause:

WITH q AS (SELECT ...)
  SELECT * FROM q CROSS JOIN q

In Rust this might look something like

...
Let {
  binding: LetId,
  value: Box<RelExpr>,
  // `expr` can refer to `value` by constructing
  // a `Get` with the appropriate LetId.
  expr: Box<RelExpr>,
},
Get { name: LetId },
...

This comes with its own set of problems, of course, for both query planning and query execution. See Why Are Query Plans Trees and Query Engines: Push vs. Pull. I have yet to see a satisfying solution to the optimization of query plans involving DAGs in this way. I think any real answer probably involves embedding an ILP solver in the optimizer.

What if we want to go further? The above two tools open up the world of directed acyclic graphs to us, but what if we want unrestricted access to represent graphs containing cycles in our programs?

There are three common ways to do this that I am aware of.

Self-Reference

SQL supports expressions referencing themselves with its WITH RECURSIVE construct:

> WITH RECURSIVE
    nums (n) AS (
        SELECT 1
     UNION ALL
        SELECT n+1 FROM nums WHERE n < 10
    )
    SELECT n FROM nums;
=>
1
2
3
4
5
6
7
8
9
10

By allowing let bindings to reference themselves, we can "close the loop" and introduce a looping edge.

Fixpoint Operator

Another way to graft recursion onto a tree-based expression language is to introduce self-reference in another way.

Part of the trickiness around constructing a self-referential expression is: how do you refer to it?

In the previous solution, we said "I'm going to give this thing a name, and put that name into scope before we begin constructing the expression itself so that the body of the expression is allowed to use it and achieve self reference." Another option is to leave a "hole" in the expression that will get filled in later on.

We can represent such a "hole" by introducing a lambda abstraction, or an anonymous function:

We might write the previous version like this in pseudocode:

let x = {1} UNION (n + 1 FOR n IN x WHERE n < 10)

This "leave a hole" version might look like this:

let nums = fn (other_nums) => { other_nums UNION (n + 1 FOR n IN other_nums WHERE n < 10) }

And then the language can provide an explicit "fixpoint" operator that takes an initial state and the lambda to iterate to close the loop for us:

let x = fix({1}, nums)

Explicit Listing of Edges

If we want the full flexibility of graph construction, we can go all the way to how something like Datalog works, where we simply write out each edge explicitly.

nums(1).
nums(n + 1) <- nums(n), n < 10.

(This is not actually valid Datalog, but is a coherent way to think about writing the program we've been using so far.)

This is a pretty big syntactic jump—we basically lose the ability to write out entire nested expressions like we do with the previous options, short of introducing some additional syntactic sugar on top to get it back. I think maybe this is part of the reason Datalog conceptually scares a lot of people off, since it eschews a lot of the things we expect from traditional programming languages in terms of syntax, making the primary point of focus in the programs the edges between operators, rather than the operators themselves. But it turns out that when you want to write graphs and not simply trees, this is a useful perspective shift, and freeing yourself from nested expressions makes graphs tenable.