Nonograms

Hello! I hope you are having a lovely day. This week I got distracted by some non-database content and it consequently took up a lot of my time. Usually I can dress these up as database-related somehow but I don't have the time this week, so it's bold-faced about puzzles.

Like many others, I was recently charmed by Every 5x5 Nonogram.

A nonogram is a type of logic puzzle not too different from a Sudoku. The result of a nonogram is a grid of black and white squares, and the constraint you have to use to solve it is a list of numbers along the rows and columns describing the contiguous chunks of cells in that row or column. For example the clue 2 4 2 attached to a row means that there is a chunk of two filled in cells, then at least one blank space, then a chunk of four filled in cells, then at least one blank space, then another chunk of two filled in cells.

To understand how to solve these, lets look at this puzzle from Every 5x5 Nonogram:

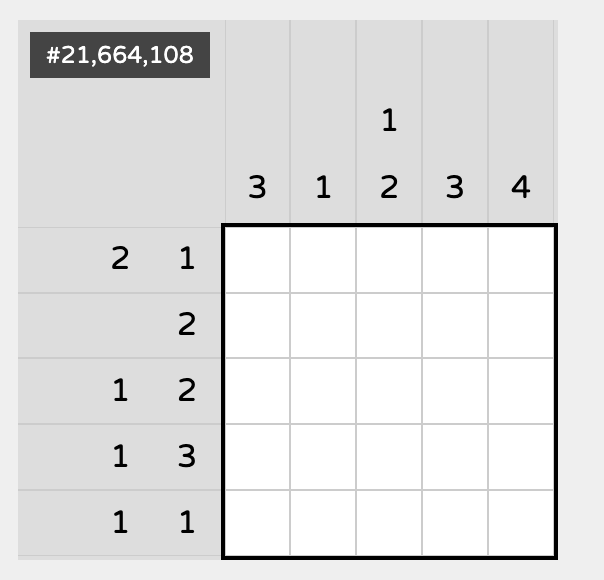
Looking at the row labelled 1 3, there's only one way to fill that row such that there is a 1-chunk then a 3-chunk:

Now a slightly harder derivation, looking at the columns labelled 3, we might notice that there are three ways to fill in a row or column with a 3: ..XXX, .XXX., or XXX... Importantly, all three of these have the middle cell filled in, so we can do that here:

We can go further and deduce that those two 1x2 blocks couldn't extend up all the way to the top row, and so the top row for both 3 columns must be empty:

We can keep making these logical deductions and come to a solved puzzle where every row and column is satisfied:

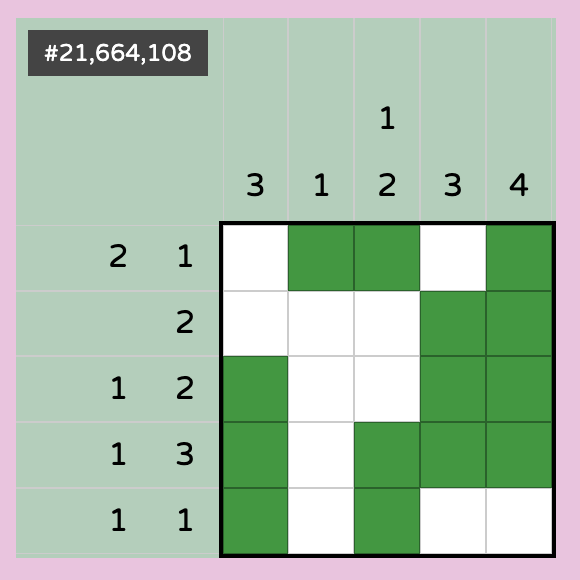
A nonogram is also sometimes called a "picross," and it might be better known to you by that name if you're a big nintendo fan. Nintendo historically really likes these, they've done a bunch:

It works pretty well for Nintendo because one of the fun parts of solving these is having a fun picture revealed at the end, and who has more beloved pixelated images than them?

The author of Every 5x5 Nonogram notes that there are 2^25= 33,554,432 possible grids, and of those, 24,976,511 are "valid" nonograms.

What does the author mean by "valid nonogram," though?

Specifically, the criterion they're using is that it can be solved in the way we did above, by looking at a single row or column at a time and then making logical deductions based on that, and then continuing to do so.

This is not the only criteria you might use though: you might say that a valid nonogram is one that has a unique solution, even if that solution is not uniquely determinable. For example, this nonogram:

      1
  21221
 2.....
12.....
 2.....
11.....
  .....

has a unique solution, but can't be solved with that method.

That method is called constraint propagation, where we take the constraints we know, infer some information, and then continue along. This was most famously described by Peter Norvig as a way to solve Sudoku puzzles.

If you allow for all puzzles that have a unique solution, you get 25,309,575 nonograms, a full 333,064 extras than you get over looking at a single slice at a time.

In full generality, some kind of backtracking search is the traditional way to solve this sort of puzzle. But since it's aimed at human solvers (for whom only "advanced" solvers typically use some kind of backtracking/guess-and-check method), we can make this algorithm explicit like so:

• pick a slice,
• enumerate all the ways that slice could be filled in that are consistent with the current fill of the puzzle,
• commit to any options (either filled or not filled) that are common to all consistent fills.
• Repeat for each slice, and repeat for as long as progress continues to be made.

This algorithm is the one that gives the 24,976,511 number. We can grow that number a bit by modifying the algorithm like so:

• pick a subset of size <= k of slices,
• enumerate all the ways those slices could be filled in that are consistent with the current fill of the puzzle,
• commit to any options (either filled or not filled) that are common to all consistent fills.
• Repeat for each <=k-subset repeat for as long as progress continues to be made.

This way, we get to consider more slices at once which gives us more power.

This lets us expand our "classes" of 5x5 nonograms:

• D1 is the class that can be solved by looking at only one slice at a time.
• Dn is the class that can be solved by looking at n slices at a time.
• U is the class of puzzles with a unique solution.

A couple observations: * D{n+1} contains everything in D{n}, since if we can solve it by looking at k slices, we can solve it by looking at k+1 slices. * D10 = U, since D10 is basically saying "consider every valid fill of the entire puzzle at once," which is equivalent to just solving the puzzle.

I won't show you my code because it's nowhere near as pretty as Norvig's and it's full of false starts and mistakes, but here's what I got:

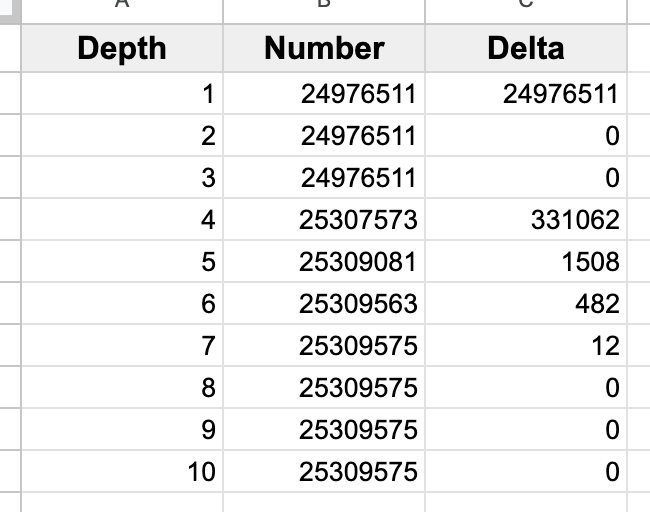
Interestingly, D2 and D3 don't grant any additional power over D1. D4 is the first place we start to see new puzzles. Here's an example of a D4 puzzle:

  2 1
  1 122
 1.....
12.....
12.....
 1.....
 1.....

Notably I think this puzzle isn't actually very hard! I think this suggests that maybe Dn isn't the best metric.

After that there's a steep dropoff in terms of the new puzzles we get. Here's a D5, D6, and D7 puzzle:

D5:

  1 2
  12121
 1.....
 3.....
21.....
 2.....
 1.....

D6:

  11
  11121
11.....
 2.....
 1.....
 2.....
 1.....

D7:

   1 11
  11111
 1.....
 2.....
11.....
 2.....
 1.....

I don't think the Dn level directly represents how hard they are for a human, but they do have some kind of correlation, since the last one is pretty tricky for sure.

Writing code for stuff this kind of constraint solver thing is the quickest way to make me feel stupid, all the alternating "for some, for all, for some, for all" that goes on is so hard for me to continually get correct and I just have endless bugs as a result. Oh well. Telling myself that's because it's actually hard!