Multiplexing

In the world of electronics, multiplexing is the process of taking a set of communication channels and collapsing them all to be transmitted along a single communication channel.

This is often represented with a diagram like this which is a pretty reasonable depiction of what's going on:

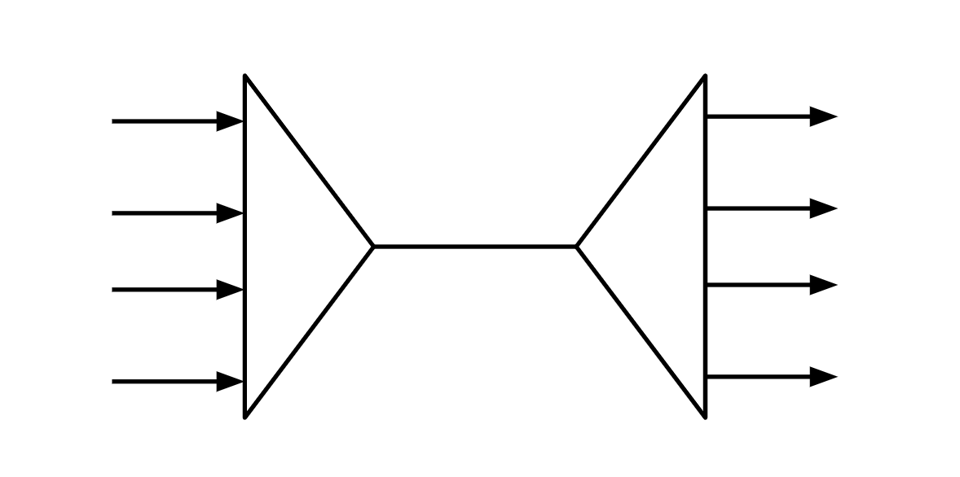
The left side is the multiplexer (sometimes called a mux), which packs the signals into a single communication line, while the right side is the demultiplexer, which explodes that single communication line into the original disparate signals.

Generally, when a signal gets put into the shared line, it is combined with some kind of key which denotes which original signal it belonged to. In the case of, say, multiplexing telephone calls over a single signal,

I want to argue that "multiplexing" in its general form is a really common pattern in a handful of nonobvious ways.

In its general form, multiplexing always has this structure:

• Associate each object in your set with some muxing key,
• send the objects along the communication channel,
• on the other end, extract the objects using the muxing key.

Bitwise Operations

One of the simplest examples of this kind of multiplexing is the use of bitmaps to encode a set of booleans. We have a collection of n booleans, we can encode them as an n-bit integer and do operations over them as though they were a single value by using bitwise operations. This has obvious efficiency gains, since CPUs can perform all of those logical operations in parallel.

We are sending multiple values (the booleans) across a single channel (the n-bit integer), indexed by a muxing key (the location in the bitmap).

Batching

It's a common need to send a request off to some service with a lookup key and get back a value for that key.

There's a certain amount of overhead associated with doing a single lookup, so people often want to send multiple keys at once, and get back multiple results in what's called a batch.

So instead of:

call(k1) -> v1
call(k2) -> v2
call(k3) -> v3

we can do

call([k1, k2, k3]) -> [v1, v2, v3]

Notice this has the same pattern: each request key is associated with a muxing key, namely its ordinal position in the array. When the results come back we can extract the value for each key.

Relational Multiplexing

Okay, so, how does any of this relate to databases. I think the most compelling example of multiplexing arises from relational databases. Imagine we have a handful of users who each have some set of rows allocated to them. We could give them each a table:

I mean, this makes sense: we have three collections, one for each user. When we get a new user, we make a new table, right?

No, of course, you'd never do it this way, you'd add a column which denotes which user a given order is associated with:

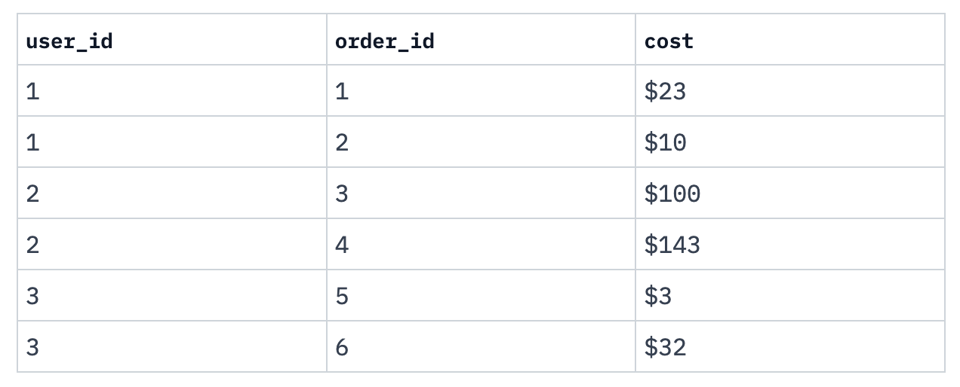
We've taken a handful of disparate information channels and coalesced them into a single information channel: we multiplexed the data from multiple tables into a single channel. In practice, if users are to be isolated enough, you'd probably want to wrap your database connections to guarantee that any particular query always restricts its queries to a single, authenticated user, and demultiplex the result.

This also extends to the physical schema, namely indexing. If you have a lexicographic indexing system (like most SQL databases support) and you prefix every index with user_id, all of your index scans can simply constrain the scan to the region which covers that particular user.

This is also how people typically build relational databases on top of KV databases: you can multiplex the entire space of relational tables onto a single key-value space: taking a single value that appears in a relational database, conceptually mapped to by the empty string:

 -> value

We can prepend a column id to the key to multiplex across rows:

<column_id> -> value

Now we exist in the space of rows. Now we can prepend a row id to multiplex across an entire table (this, in practice would be the value of the row's primary key):

<row_id>/<column_id> -> value

Then, to account for multiple tables, we can prepend a table id:

<table_id>/<row_id>/<column_id> -> value

and now we've multiplexed an entire relational database, with structure, across a KV-database that lacks structure.

Relational multiplexing is particularly cool because it composes. You can repeat this process any number of times, with the muxing key of one level just being data at a higher level. This lack of distinction between the muxing key and the data is particularly noteworthy for the application of decorrelation.

Query Decorrelation

Query decorrelation is the process of turning a correlated subquery (which is a subquery that has free variables) into a join:

CREATE TABLE ab (a INT PRIMARY KEY, b INT);
CREATE TABLE xy (x INT PRIMARY KEY, y INT);

SELECT (SELECT y + b FROM xy WHERE a = x) FROM ab;

This query says that for each row in ab, we want to compute the result of (SELECT y + b FROM xy WHERE a = x), which is itself a relation. We happen to know that there will be at most one row in that relation, since in this context a is a constant (because it is free), and x is the primary key of xy. So we don't have to worry about the result having multiple rows, but we do have to worry about the result possibly not being present (in which case the result should be NULL).

How can we pack all of these relations into a single relation? We need a mux key.

Note that the value of this expression, (SELECT y + b FROM xy WHERE a = x), is entirely determined by its free variables (those not bound by a table being queries), {a}. This suggests we probably want to use a as our mux key. So we want to take each of these relations, add a new column named a that corresponds to the value of a, and then the outer query can just pluck out the subsets it wants with a join.

We have the set of all a values we'll need—it's the ones that are present in ab. So we can compute this with a join:

SELECT a AS mux, x, y FROM xy, ab WHERE mux = x

Then a level up, we select the value we want by left joining to ab (we use a left join because if there wasn't a corresponding row we want a NULL instead of the row not showing up):

SELECT y + b FROM (
  ab
  LEFT OUTER JOIN
  (SELECT a AS mux, x, y FROM xy, ab WHERE mux = x)
) ON mux = a

From here, now that we've completely eliminated any correlation, we can get to the natural result of the query by doing some simplifications:

Unfold the join:

SELECT y + b FROM
  ab
  LEFT OUTER JOIN
  ((SELECT a AS mux FROM ab),
    INNER JOIN ON mux = x
  xy)
ON mux = a

Commute the joins a bit:

SELECT y + b FROM
  (SELECT mux, a, b FROM (SELECT a AS mux FROM ab), ab WHERE mux = a)
  LEFT OUTER JOIN
  xy
ON a = x

Eliminate the self-join:

SELECT y + b FROM
  ab LEFT OUTER JOIN xy
ON a = x

To get the final result:

SELECT y + b FROM (ab LEFT OUTER JOIN xy ON a = x)

Which doesn't have any correlation.

This is not the most direct way to get to that result, but it is a way to understand what is happening here.

These are a bunch of similar ideas that are all sort of unified by the idea of "multiplexing" and this pattern shows up a lot.