Linearity in Query Processing

I saw a fun post this week about interpreting colours as vectors and the way you can exploit that interpretation to nicely represent certain operations you might want to do on those colours.
As the author notes, you can perform an operation on a colour via a matrix multiplication if and only if that operation is linear. Linear maps obey
and
One of the first things you learn about matrices (and oftentimes how they’re motivated in the first place) is that linear maps are 1:1 with matrices: an operation on a vector can be performed by multiplying that vector by a matrix if and only if its linear.
In query processing, an operator is called linear if it satisfies
where R and S are bags of rows (and sometimes “Z-multisets”).
We don’t need to specify the scalar multiplication property since, for the multiplicities people usually use (N or Z), it’s implied:
But if you were working with a fancier kind of multiplicity you’d require that as well.
If you played around with the relational derivative, you might have noticed that some derivatives, like those for projections and inner joins, have the property that they don’t refer to the existing values in the table at all. It’s sufficient to just look at the new rows to determine what the changes will be. This is in contrast to the right side of a left outer join or a DISTINCT operator, which will have a term for the existing values in the table.
This distinction is exactly linearity, and the analogy to linearity in linear algebra is very natural: to know how a linear operator will affect a particular vector, it suffices to know how it impact all of the basis vectors that make up that vector. To know how a linear operator will affect a relation, it suffices to know how it affects each individual row.
These notions being the same suggests an interesting perspective on what a relation even is, which is that they’re vectors in some vector space spanned by the set of all possible rows. If that’s true, then all of our linear operators, Projection, Selection, Join, should all have corresponding matrices which, when multiplied by the relation-vector, apply the corresponding relational linear map.
And indeed this is true!…but, maybe not in the most satisfying or computationally useful way. Since this vector space is spanned by the (probably) infinite set of all rows, the corresponding matrices are all infinite, indexed by the sets of rows, and are not particularly structurally interesting.
The selection matrix is just the identity matrix with some 1s replaced with 0s whenever the row for that position doesn’t meet the predicate:
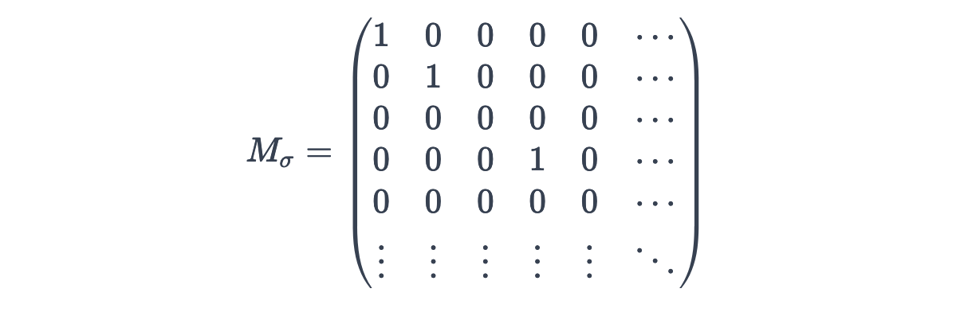
The projection matrix maps each row to some new row, so it has exactly one 1 in each column:

You can figure out for the “join with S” matrix looks like.
Despite this descent into infinite matrices that don’t have much practical use, the notion of linearity is pretty useful when thinking about query processing. It is precisely the linear operators that can be distributed nicely and pushed down across arbitrarily sharded databases, since you don’t need access to the rest of the database to compute them. Linear operators are closed under composition, tend to commute with each other, and are generally just easy to work with. Of course, much of the interesting computation happens around the non-linear operators.
For a more in-depth treatment of the notion of linearity, see Guido Moerkotte’s work in process book on query compilers.
Add a comment: