Infinite Relations

Let's write a super simply query engine using the iterator model. Something like this is conceptually what the compilation target for something like SQL generally looks like.
Our iterators will be nextable, and return None when they're exhausted. We can construct an iterator over some fixed set of values easily:
class ConstIter:
def __init__(self, rows):
self.i = 0
self.rows = rows
def next(self):
if self.i >= len(self.rows):
return None
self.i += 1
return self.rows[self.i-1]
it = ConstIter([1, 2, 3])
print(it.next())
print(it.next())
print(it.next())
print(it.next())
1 2 3 None
Of course, the value of this model is that it's composable: we can derive iterators from other iterators, like having a Filter iterator that only allows rows through meeting some predicate:
class Iter:
def filter(self, p):
return FilterIter(self, p)
class FilterIter(Iter):
def __init__(self, it, p):
self.it = it
self.p = p
def next(self):
while True:
n = self.it.next()
if n == None:
return None
if self.p(n):
return n
class ConstIter(Iter):
def __init__(self, rows):
self.i = 0
self.rows = rows
def next(self):
if self.i >= len(self.rows):
return None
self.i += 1
return self.rows[self.i-1]
it = ConstIter([1, 2, 3]).filter(lambda x: x % 2 == 1)
print(it.next())
print(it.next())
print(it.next())
1 3 None
We can also easily take the union of two iterators by reading all the values from one followed by all the values of the other:
class UnionIter(Iter):
def __init__(self, a, b):
self.a = a
self.b = b
def next(self):
n = self.a.next()
if n != None:
return n
return self.b.next()
it = ConstIter([1,2,3]).union(ConstIter([10,20,30]))
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
1 2 3 10 20 30 None
It's also very easy and handy to transform all of the elements in an iterator:
class MapIter(Iter):
def __init__(self, it, f):
self.it = it
self.f = f
def next(self):
n = self.it.next()
if n == None:
return None
return self.f(n)
it = ConstIter([1,2,3]).map(lambda x: x * 10)
print(it.next())
print(it.next())
print(it.next())
print(it.next())
10 20 30 None
Another useful primitive for such a query engine to have is a product operator, which takes two iterators and emits their cross product. This is actually a little trickier than it might seem, because we have no way to reverse our iterators: we can only next them. This means we have to buffer up the rows from the left iterator so that we can maintain a pointer into it, but this isn't a big deal:
class ProductIter(Iter):
def __init__(self, a, b):
self.a_rows = []
n = a.next()
while n != None:
self.a_rows.append(n)
n = a.next()
self.a_idx = 0
self.b = b
self.cur_b = b.next()
def next(self):
while True:
if self.cur_b == None:
return None
if self.a_idx >= len(self.a_rows):
self.a_idx = 0
self.cur_b = self.b.next()
else:
r = (self.a_rows[self.a_idx], self.cur_b)
self.a_idx += 1
return r
it = ConstIter([1, 2, 3]).product(ConstIter([4,5,6]))
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
(1, 4) (2, 4) (3, 4) (1, 5) (2, 5) (3, 5) (1, 6) (2, 6) (3, 6) None
One observation we might have without thinking too hard is that we need not be restricted to our relations being finite here. We could write the following iterator:
class NatIter(Iter):
def __init__(self):
self.i = 0
def next(self):
self.i += 1
return self.i - 1
it = NatIter()
print(it.next())
print(it.next())
print(it.next())
print(it.next())
0 1 2 3
And everything will work great! We can filter this happily:
it = NatIter().filter(lambda x: x % 2 == 1)
print(it.next())
print(it.next())
print(it.next())
print(it.next())
1 3 5 7
And we can join a concrete list against it:
it = ConstIter(["justin", "smudge", "sissel"]).product(NatIter())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
print(it.next())
('justin', 0) ('smudge', 0) ('sissel', 0) ('justin', 1) ('smudge', 1) ('sissel', 1) ('justin', 2) ('smudge', 2)
Out of the tools we have, we can take our NatIter and from it, construct the negative numbers:
it = NatIter().map(lambda x: -x - 1)
print(it.next())
print(it.next())
print(it.next())
print(it.next())
-1 -2 -3 -4
And, I learned this in school: to get the integers, we can just take the union of the natural numbers and the negative numbers!
neg = NatIter().map(lambda x: -x - 1)
ints = NatIter().union(neg)
print(ints.next())
print(ints.next())
print(ints.next())
print(ints.next())
Oh...
0 1 2 3
That seems...probably wrong. The issue is with our implementation of UnionIter: we're only looking at the second iterator once our first iterator is completely exhausted, which, in this case, since the first iterator is infinite, will never happen!
There's a way to make precise the fact that this implementation is wrong: when we take the union of two iterators, we want it to be true that if we would eventually get x by calling next on one of the iterators in isolation, we should eventually get x by calling next on the union. The reason this is a useful correctness condition is because it suggests that nothing can be "infinitely delayed." If there's something we need to hit, then we are assured that if we go long enough, we will hit it.
It's easy to see that this condition is not true for our current implementation of union: if we called next on neg, we would immediately hit -1, but calling next on our union, we will never get it.
This is easy to fix by changing the implementation of union to interleave the two iterators, rather than concatenate them:
class UnionIter(Iter):
def __init__(self, a, b):
self.a = a
self.b = b
def next(self):
self.a, self.b = self.b, self.a
return self.b.next()
Now, when we compute our union:
neg = NatIter().map(lambda x: -x - 1)
ints = NatIter().union(neg)
print(ints.next())
print(ints.next())
print(ints.next())
print(ints.next())
0 -1 1 -2
We see we get a "fair" enumeration of both iterators.
What we've done is actually construct a proof that the integers are countable: that they can be mapped 1-to-1 with the natural numbers.
It's less obvious how to fix our product operator. If we run this:
pairs = NatIter().product(NatIter())
print(pairs.next())
print(pairs.next())
print(pairs.next())
print(pairs.next())
Our program doesn't even run: we're trying to buffer all of NatIter, which will never finish. But, even if we could solve that problem, we would still have another: the intention for product is that we enumerate every pair between the two inputs, and we can visualize this by an infinite two-dimensional grid:
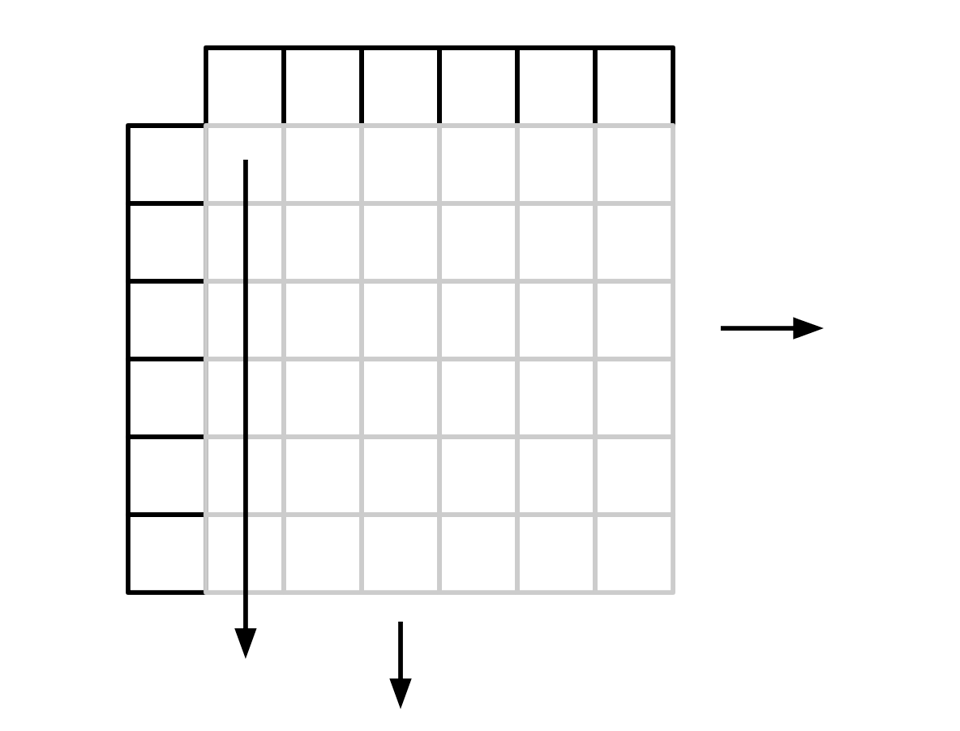
The problem is that the way our program works now, we will only enumerate along the leftmost arrow, and never see anything to the right of it.
We can borrow another trick from the theory of countable sets to solve this.
The problem right now is that we've divided this infinite grid up into an infinite set of infinite columns. Which means that if we want to enumerate all of the cells, we must first enumerate all of a column, which is, again, infinite. A better (and common, in this world) thing to do is to break up the grid into an infinite list of finite diagonals:
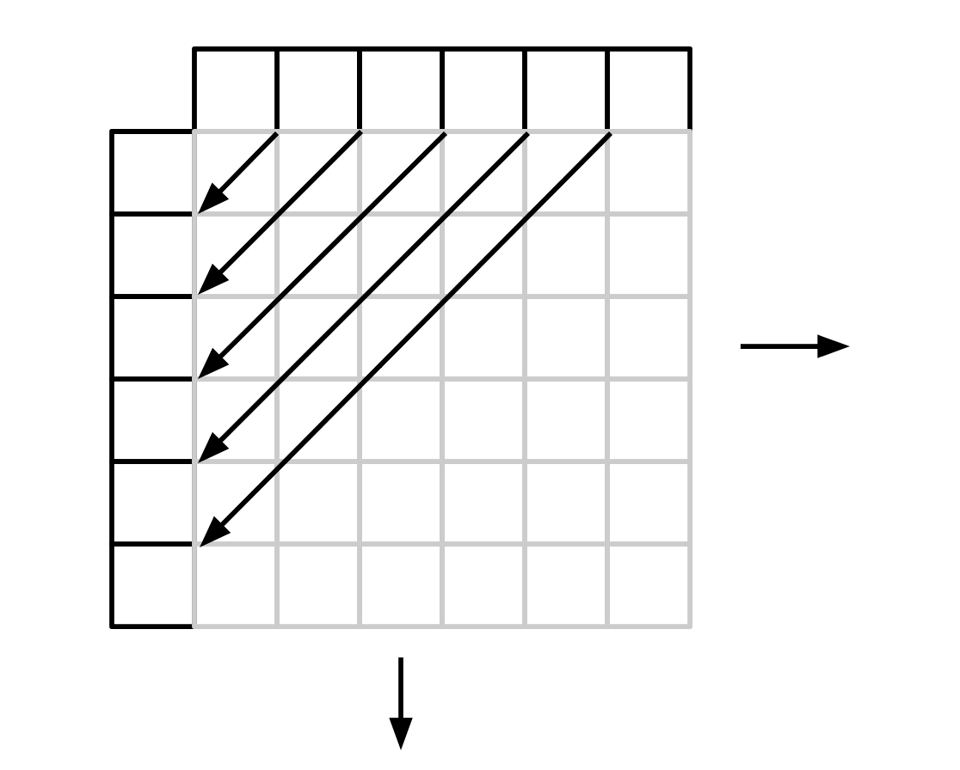
If we go through each diagonal in turn, we're guaranteed that we'll hit every square eventually.
For our purposes it will be a little simpler to traverse the grid like this, by continually growing rectangles, but the result is the same:
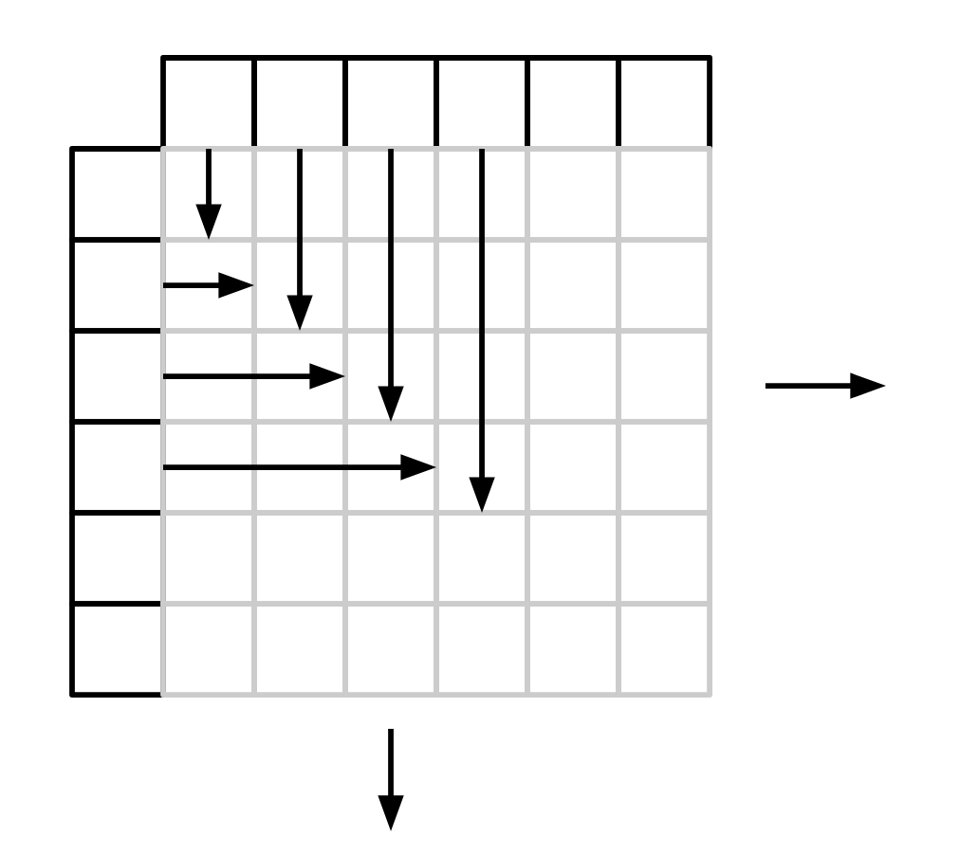
It's a little ugly to implement this traversal so I'm going to hide my implementation behind a gist link, if you have a really nice way let me know. The result is that we can iterate over our joined natural number relations just fine:
pairs = NatIter().product(NatIter())
print(pairs.next())
print(pairs.next())
print(pairs.next())
print(pairs.next())
print(pairs.next())
print(pairs.next())
print(pairs.next())
print(pairs.next())
print(pairs.next())
(0, 0) (1, 0) (0, 1) (1, 1) (2, 0) (2, 1) (0, 2) (1, 2) (2, 2)
This is a useful tool for logic programming, where we might have these iterators computing some nontrivial result.
Add a comment: