May 5, 2025

How To Understand That Jepsen Report

There is a new Jepsen report which, as always, is an entertaining read and gives some insight into the way things might be broken in subtle ways.

I learned some interesting things reading this report and I figured it might be helpful to share them as far as understanding what exactly the breakage they report is.

If you want more detail on this, I recommend Concurrency Control and Recovery in Database Systems which Phil Eaton is running a book club for right now.

The dependency graph of a transactional history communicates the implied ordering between committed transactions in a history.

• If T2 reads a value that T1 wrote, T2 must come after T1 (a write-read, or wr dependency).
• If T3 reads a key and doesn't observe a value that T1 wrote to that key, T3 must come before T1 (a read-write, or rw or anti-dependency. I don't know why they're called "anti" dependencies but they are special and so they're sometimes denoted with a dashed arrow).
• If T4 overwrites a value that T1 wrote, T4 must come after T1 (a write-write, or ww dependency).

We can represent this in a graph like so:

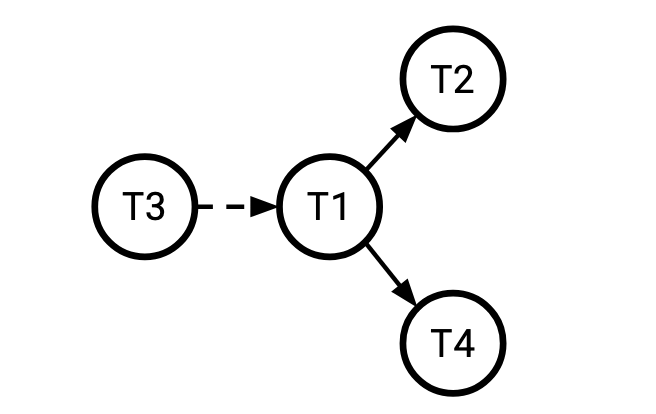
A history is serializable if this graph is acyclic. You might see a different definition elsewhere, often people like to say it's serializable if it's equivalent to some serial order, but these definitions are equivalent because a directed graph is acyclic if and only if it permits a topological sort, which is the same as saying it's equivalent to a serial order.

This is a lovely definition but it obviously doesn't really extend to lower isolation levels which, by definition, permit some cycles (otherwise they'd be as restrictive as serializable) but place some restrictions on which cycles are allowed.

Snapshot Isolation

Snapshot isolation is an isolation level where transactions are allowed to operate on a "consistent snapshot" of the database. The definition of snapshot isolation I'm used to is:

• Every committed transaction has a read timestamp Tr and a write timestamp Tw. The set of all timestamps is totally ordered, with a transaction's Tr always preceding its Tw.
• A committed transaction can see the writes of any other committed transaction whose write timestamp precedes its read timestamp.
• Two transactions are concurrent if their [Tr, Tw] intervals overlap. Two concurrent committed transactions never write to the same key.

Note that we're not being so explicit as to require that the timestamps reflect real-time, or are integer points in time, or anything, all we're saying is that there is some set of objects called "timestamps" that allow for a total order and agree with the read and write dependencies between transactions.

Serializable is a special case of this where Tr=Tw for all transactions. Snapshot isolation is thus weaker than serializability: it is vulnerable to write skew. The simplest example of write skew is the following:

• T1 reads register x and copies its value to y.
• T2 reads register y and copies its value to x.

In any serial execution of these two transactions, the end result will be x and y containing the same value. In snapshot isolation, a third outcome is possible: the two values swap. This is possible under the ordering T1r < T2r < T1w < T2w.

It's not obvious how to characterize what is and is not allowed under snapshot isolation in terms of dependency cycles between the transactions. Note that we can no longer simply say "the dependency graph cannot have cycles." This is a dependency cycle: T1 depends on T2 and T2 depends on T1, but the outcome is legal (and would not be at the serializable isolation level).

Making Snapshot Isolation Serializable (FLOOS) showed that any cycles in the dependency graph of a snapshot history must have two consecutive rw edges, or anti-dependencies. This means that given a cycle in a dependency graph, if it's a legal snapshot history, then you can find two consecutive rw edges in it.

In FLOOS, this fact is used to bootstrap serializability from snapshot isolation: they observe that this means that if the graph contains no consecutive anti-dependency edges, then no cycles can exist at all, and thus the history is serializable. This observation was later used to graft serializability onto Postgres by prohibiting those "dangerous structures."

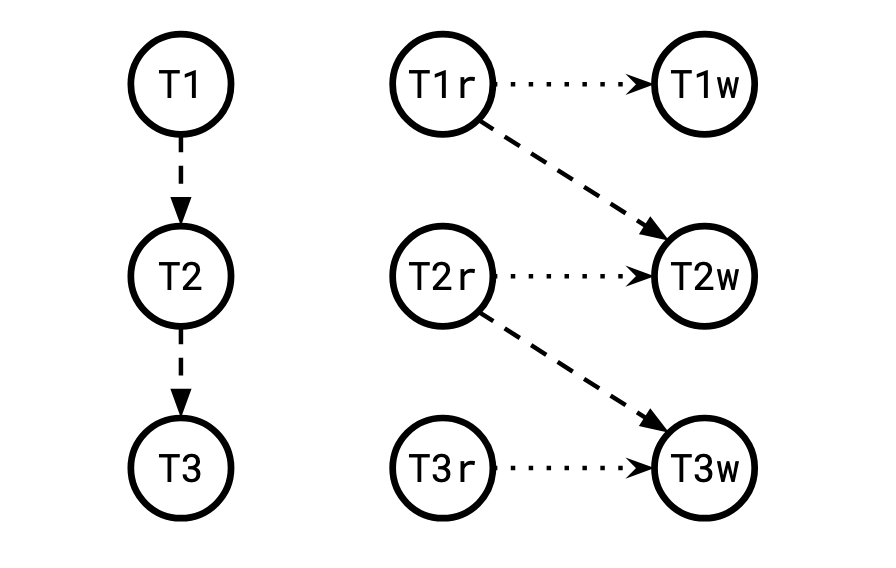
This sounds arcane but it's actually quite simple why this restriction exists. To see why, consider the graph that is not over the transactions, but over the read and write timestamps. Replace each transaction vertex with a pair of read and write vertices, with read -> write:

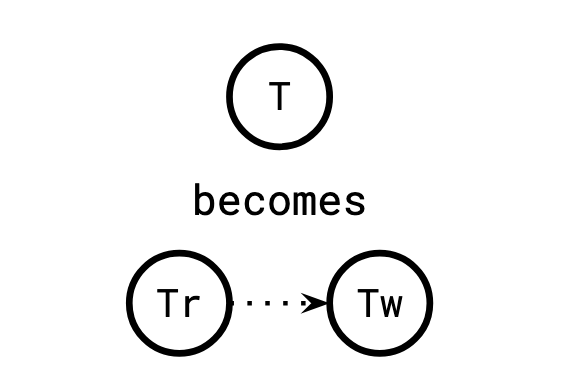
We can invert this operation to recover the original graph by contracting all of the edges we introduced this way.

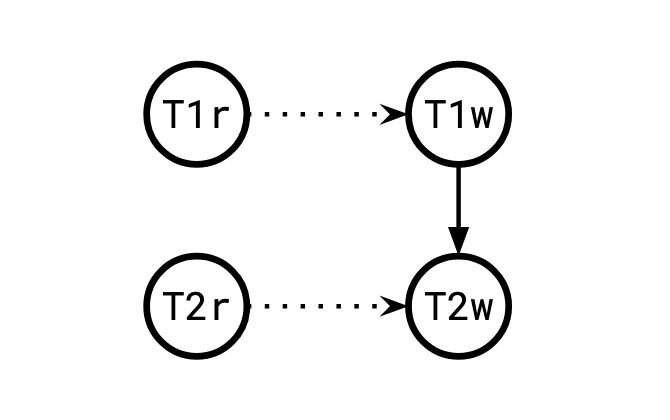
Let's look at what each of the kinds of transactional dependencies looks like under this model:

ww dependency

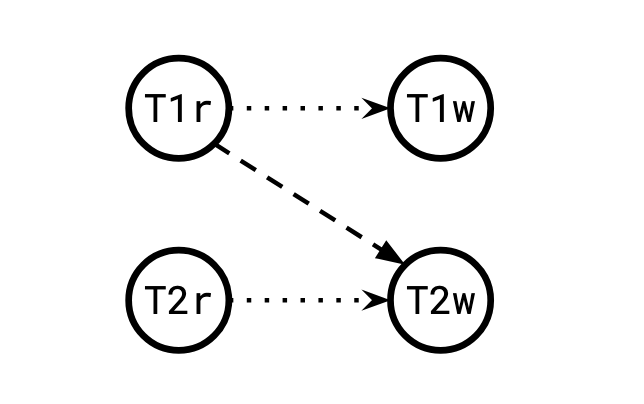
rw (anti) dependency

wr dependency

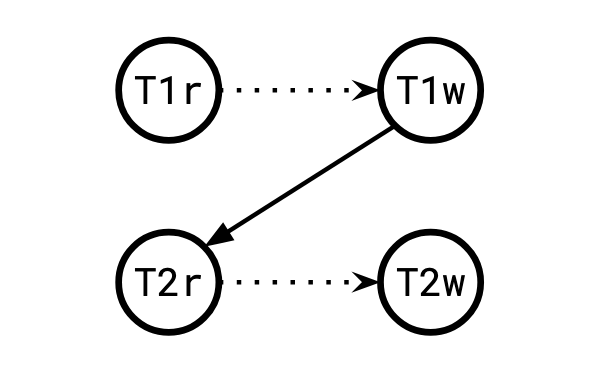
Of these, rw-dependencies are special because two rw-dependencies in a row is the only pattern that doesn't preserve paths from the original dependency graph. Try other patterns and you'll see this is true.

Notice that in the smaller dependency graph on the left, there is a path from T1 to T3, but in the expanded RW-dependency graph, there isn't.

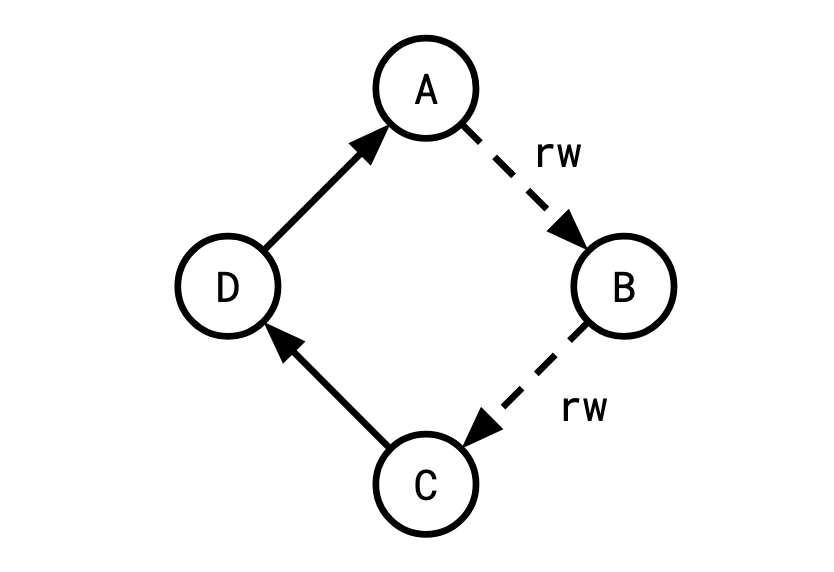
Remember we're trying to see why something that is illegal in serializable (a cycle) would be legal in snapshot. Say we have the following cycle in our serialization graph (so by definition, it's illegal under serializable):

To see why snapshot isolation can't prevent this, let's zoom in on B and split it into its constituent read and write vertices:

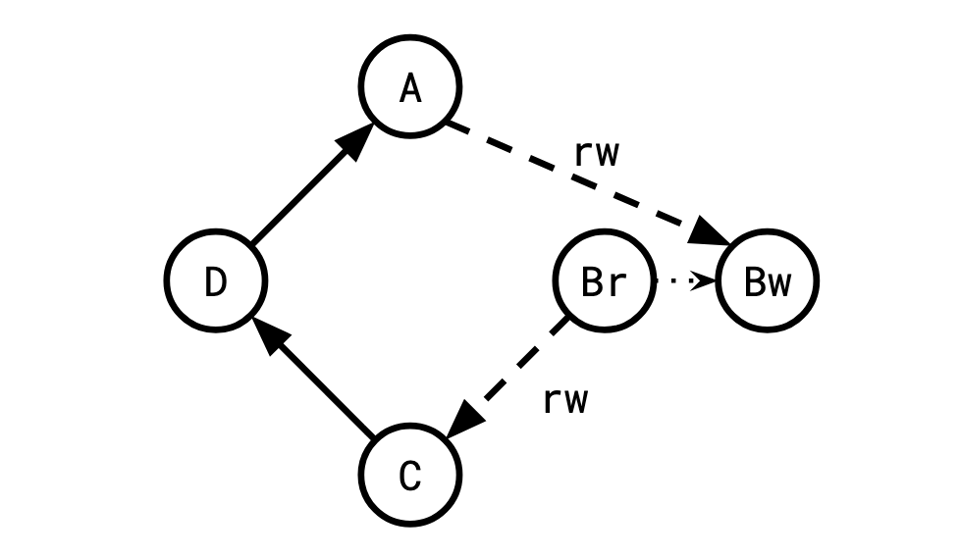
The cycle disappeared! Because rw edges always end at a W vertex and start at a R vertex, cycles aren't maintained through two of them in succession because the internal edge goes from R to W.

This is why the above graph is illegal under serializable but legal under snapshot: serializable can "see" the cycle, but snapshot is blind to it because it splits up the reads and the writes.

Jepsen

Now that we have the background knowledge on serializability and snapshot isolation, we can get into the Jepsen report.

Let's examine in detail the anomaly that Jepsen reports using the framework above.

From top to bottom, call these transactions T1, T2, T3, and T4. T1 appended 9 to row 89, resulting in the list [4 9], which T2 observed. T3 appended 11 to row 90, resulting in the list [11]. That version was overwritten by T4, which appended 3 to row 90, and read the resulting list [11, 3]. While T2 observed T1’s append to row 89, it failed to observe T3’s append to row 90. Symmetrically, T4 observed T3’s append to row 90, but failed to observe T1’s append to 89.

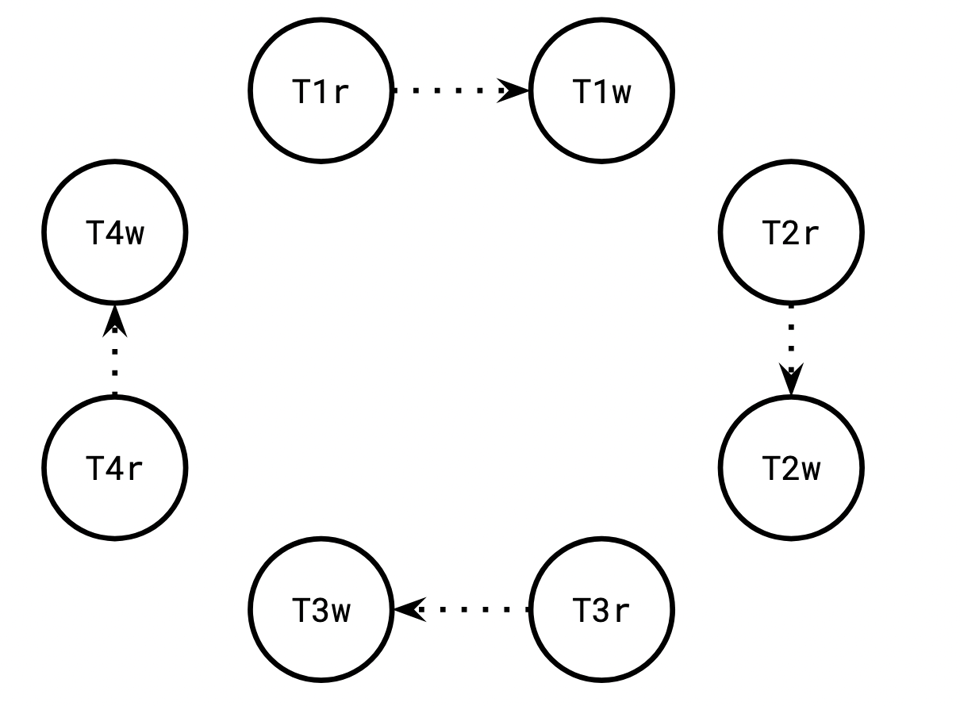
We start with four transactions, T1 through T4. We can begin our dependency graph like that:

From top to bottom, call these transactions T1, T2, T3, and T4.

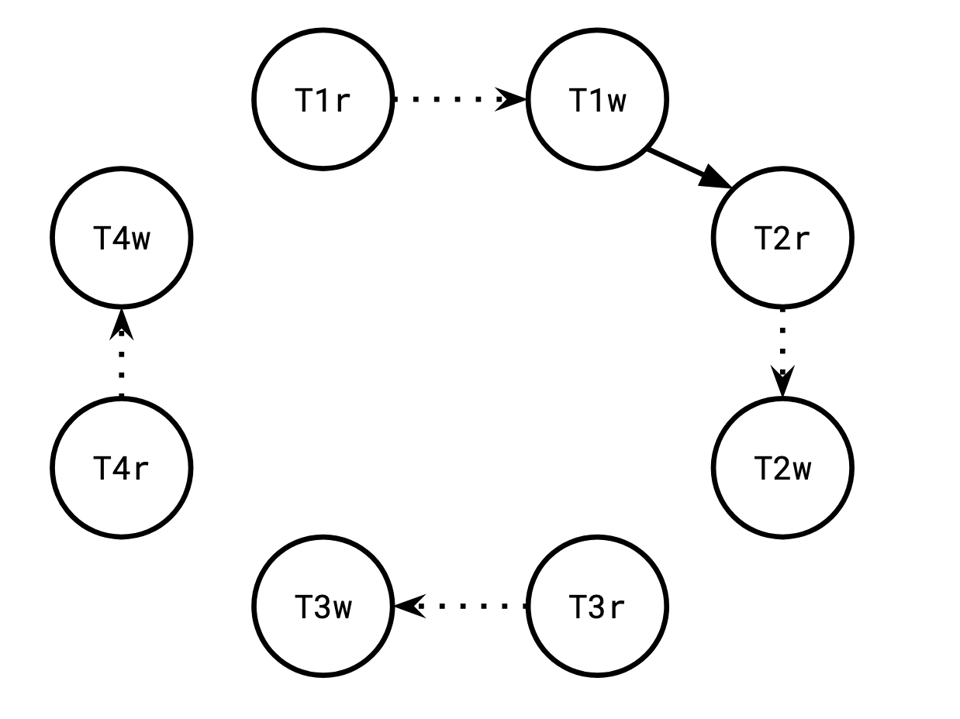
T1 appended 9 to row 89, resulting in the list [4 9], which T2 observed.

This induces a wr edge from T1 to T2:

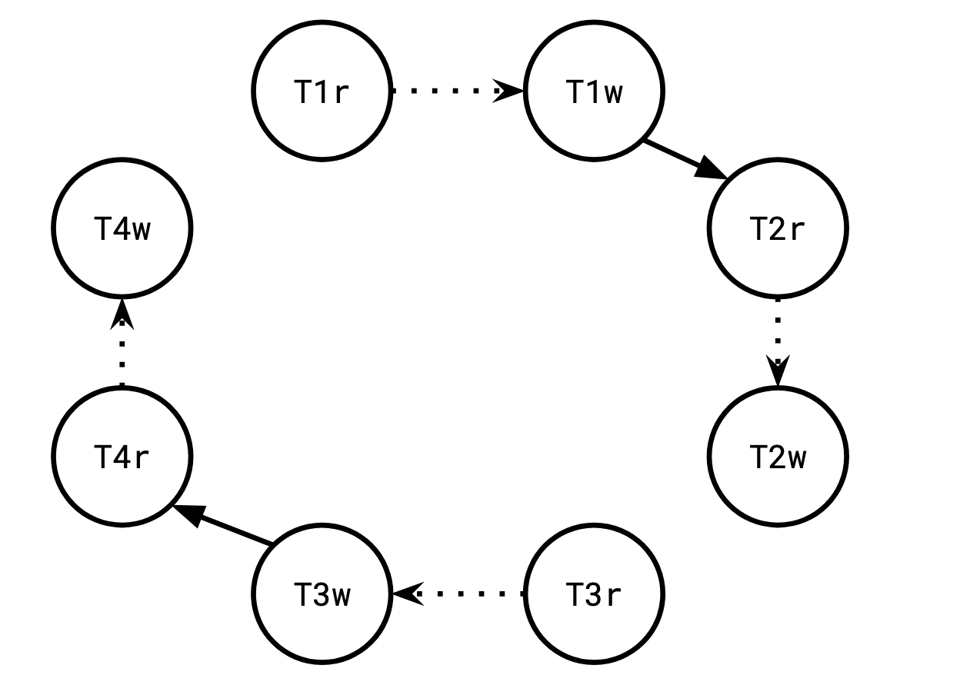
T3 appended 11 to row 90, resulting in the list [11]. That version was overwritten by T4, which appended 3 to row 90, and read the resulting list [11, 3].

Since T4 read a value T3 wrote, we have another wr edge, from T3 to T4:

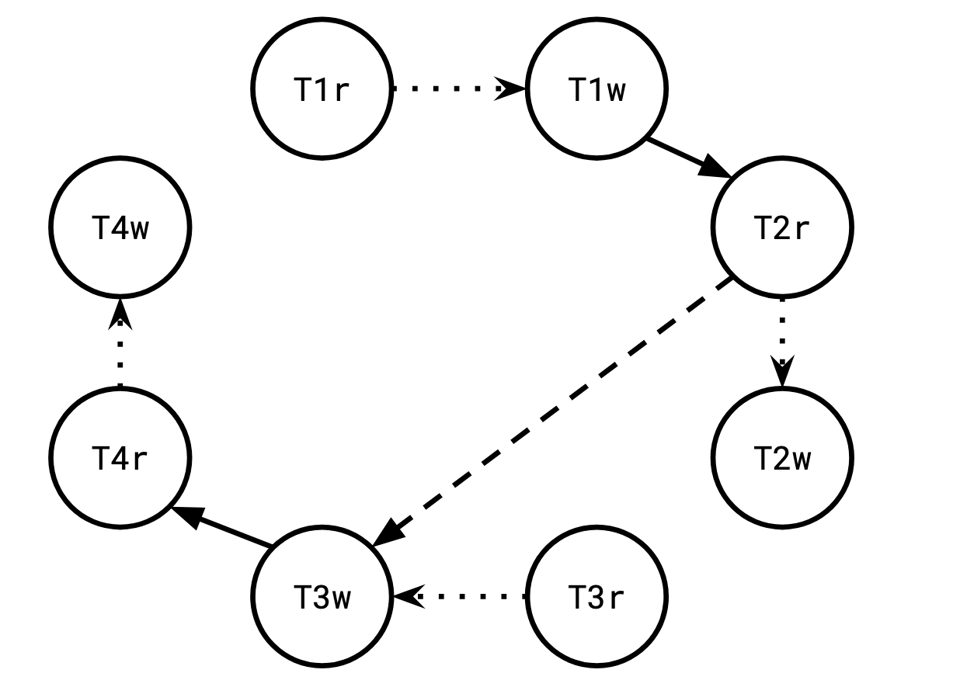
While T2 observed T1’s append to row 89, it failed to observe T3’s append to row 90.

Since T2 did not observe T3's write, there is a rw edge from T2 to T3 (because T2r must have preceded T3w):

Symmetrically, T4 observed T3’s append to row 90, but failed to observe T1’s append to 89.

Finally, T1w must have come before T4r, because T4 didn't observe T1's write:

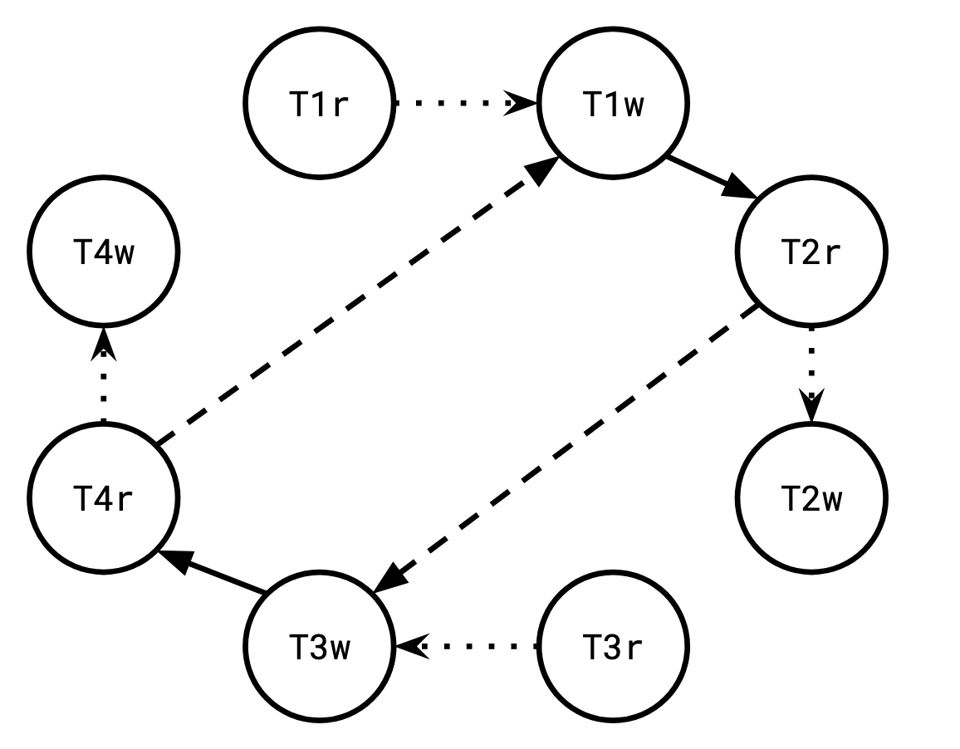
And boom, we have a cycle! And thus a snapshot isolation violation, because this cycle precludes putting a total order over the vertices that respects their dependencies.

But Jepsen didn't talk about it this way: they said that they observed "G-nonadjacent:"

Since this cycle includes read-write dependencies which are not adjacent to each other, this cycle is G-nonadjacent, a violation of Snapshot Isolation.

So what's the difference?

Because Jepsen is based around finding structures in graphs to detect illegal behaviour, they cleverly use the contrapositive of this observation to detect snapshot isolation violations:

FLOOS Statement: If a history is a legal snapshot history, then every cycle in its dependency graph contains two consecutive anti-dependency edges.

Contrapositive Used By Jepsen: If there's a cycle in the dependency graph that doesn't have two consecutive anti-dependency edges, the history is not a legal snapshot history.

I think the Jepsen claim could be expressed a bit more unambiguously as:

Since this cycle includes read-write dependencies and does not contain two which are adjacent to each other, this cycle is G-nonadjacent, a violation of Snapshot Isolation.

The Jepsen page on G-nonadjacent defines:

Phenomenon G-nonadjacent, or Non-adjacent Anti-dependency Cycle, is Jepsen’s term for one type of G2: a dependency cycle involving read-write edges. Specifically, G-nonadjacent is a dependency cycle made up of any number write-write and write-read edges, and at least one read-write edge (also known as an anti-dependency) and no two read-write edges are adjacent to one another.

G-nonadjacent is a Jepsen-ism used to allow for this definition of snapshot isolation.

There might be a little bit of logic-juggling you have to do to make this make sense: FLOOS says "every legal bad thing looks like this," and Jepsen thus infers "if there's a bad thing that doesn't look like that, it's not legal." To keep things straight, from the perspective of validating serializability, the two consecutive rw edges are bad (FLOOS calls them "dangerous structures" for this reason), they are what permit non-serializable behaviour. From the perspective of validating snapshot isolation, they're good: they mean the bad thing observed was actually allowed.

Note that it seems to me defining Snapshot this way, with Jepsen's definition of snapshot isolation:

Phenomenon G-nonadjacent, or Non-adjacent Anti-dependency Cycle, is Jepsen’s term for one type of G2: a dependency cycle involving read-write edges. Specifically, G-nonadjacent is a dependency cycle made up of any number of write-write and write-read edges, and at least one read-write edge (also known as an anti-dependency) and no two read-write edges are adjacent to one another.

[...]

These adjacent read-write edges are the cycles which Snapshot Isolation allows. However, Jepsen is not aware of an extant name for their inverse—those cycles which Snapshot Isolation prevents. Based on the literature and communications with Peter Alvaro & Alexey Gotsman, Jepsen calls this inverse phenomenon G-nonadjacent.

operates as though the FLOOS statement is actually if-and-only-if:

Original Statement: If a history is a legal snapshot history, then every cycle in its dependency graph contains two consecutive anti-dependency edges.

Jepsen interpretation: A history is a legal snapshot history if and only if every cycle in its dependency graph contains two consecutive anti-dependency edges.

Converse (Jepsen definition of Snapshot): If every cycle in the dependency graph contains two consecutive anti-dependency edges, then the history is a legal snapshot history.

This is a bit weaker than most working definitions of snapshot isolation because it doesn't prohibit overlapping write sets between concurrent transactions. This is fine: it's actually good for Jepsen to use a weaker model than most working models so that any anomalies they find apply to the largest possible set of consumers.

It's also important to remember that Jepsen happily will take a weaker definition because Jepsen is not in the business of proving systems correct, it is only concerned with providing proof that a system is incorrect, or with noting its inability to find such proof (which does not constitute a proof of correctness).

---

This stuff is subtle and contentious, any mistakes in this post are mine! But it was made clearer and more rigorous through some discussion with Alex, Phil, Shachaf, and Ilia.