Discrete Distributions

For a while now, my favourite piece of technical writing has been Darts, Dice, and Coins: Sampling from a Discrete Distribution by Keith Schwarz. In it, he answers this question:

You are given an n-sided die where side i has probability p_i of being rolled. What is the most efficient data structure for simulating rolls of the die?

He covers a bunch of fun sampling techniques in pursuit of building up to the alias method, an algorithm that lets you sample from a such a distribution in (maybe surprisingly) constant time!

I want to talk about one of the approaches he discusses, which is using a binary search tree to simulate a distribution. The idea is that if we represent our distribution as a sorted list of cumulative probabilities, we can generate a float in [0, 1) and then binary search the list to find the distribution that corresponds to that float:

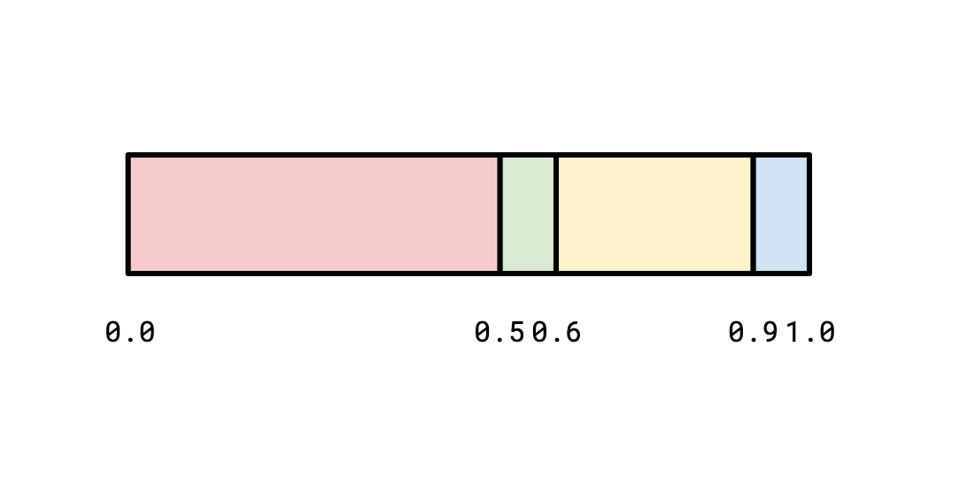
If we generate a value of 0.78, we can binary search the list of boundaries to figure out that we landed in the yellow region in logn time.

Keith points out we can represent this binary search as a tree, which presents an interesting opportunity: since we very frequently will be sampling from the red area, we probably don't want a balanced tree, like we would in a situation where we expected all of our outcomes to be equally sampled.

Keith observes that this is exactly the Optimal Binary Search Tree problem, which is well studied, and such tree can be built in O(n^2) time. I want to point out that with a slight change to the setup, we can build similar (also in some sense optimal) trees much faster, in O(nlogn) time, with a simple algorithm.

Huffman Coding

A prefix binary code is a mapping from characters to binary sequences of zeroes and ones which is prefix-free, meaning none of the binary sequences which characters map to are prefixes of one another. An example of such a prefix-free code is:

A -> 0
B -> 100
C -> 101
D -> 110
E -> 111

The fact that no code is a prefix of another means that we can decode an encoded sequence with the following algorithm:

n := 1
for len(input) > 0 {
  if input[:n] is a code {
    emit encodings[input[:n]]
    input = input[n:]
  }
  i += 1
}

We never have to do any kind of hedging in case an encoding might actually be some different character, since because it's prefix-free, once we recognize a character we know for sure that that was the one that was encoded.

The reason you might, in theory, want to do this kind of variable-length encoding of text is that the frequencies of various characters might be very imbalanced. If the typical text we're trying to encode has a lot of As and not very many Ds, we want A to be encoded with a shorter code than D so that the resulting encoded string is as short as possible.

One obvious trick we can do to understand this problem better is to nail down what "prefix-free" actually means. We can model a prefix-free code as a binary tree, where we take a left subtree for each 0 in the code and a right subtree for each 1 in the code, and each character is a leaf:

One interesting thing about this representation is that it's bijective. Every prefix-free code can be represented in this way, and every tree like this represents a prefix-free code. This means that if we can translate our problem into the language of trees, and solve it there, we can rest easy knowing that that solution will translate losslessly into the world of prefix-free codes.

So, the optimal prefix coding problem is, given an alphabet, and given the frequencies of characters appearing in the source text, come up with an encoding the minimizes the expected length of the encoded text.

The following Huffman Coding Algorithm computes such an optimal code:

• Start with each character of your alphabet paired with their frequency (f, C).
• Take the two characters with the lowest frequency and join them together and add their frequencies:

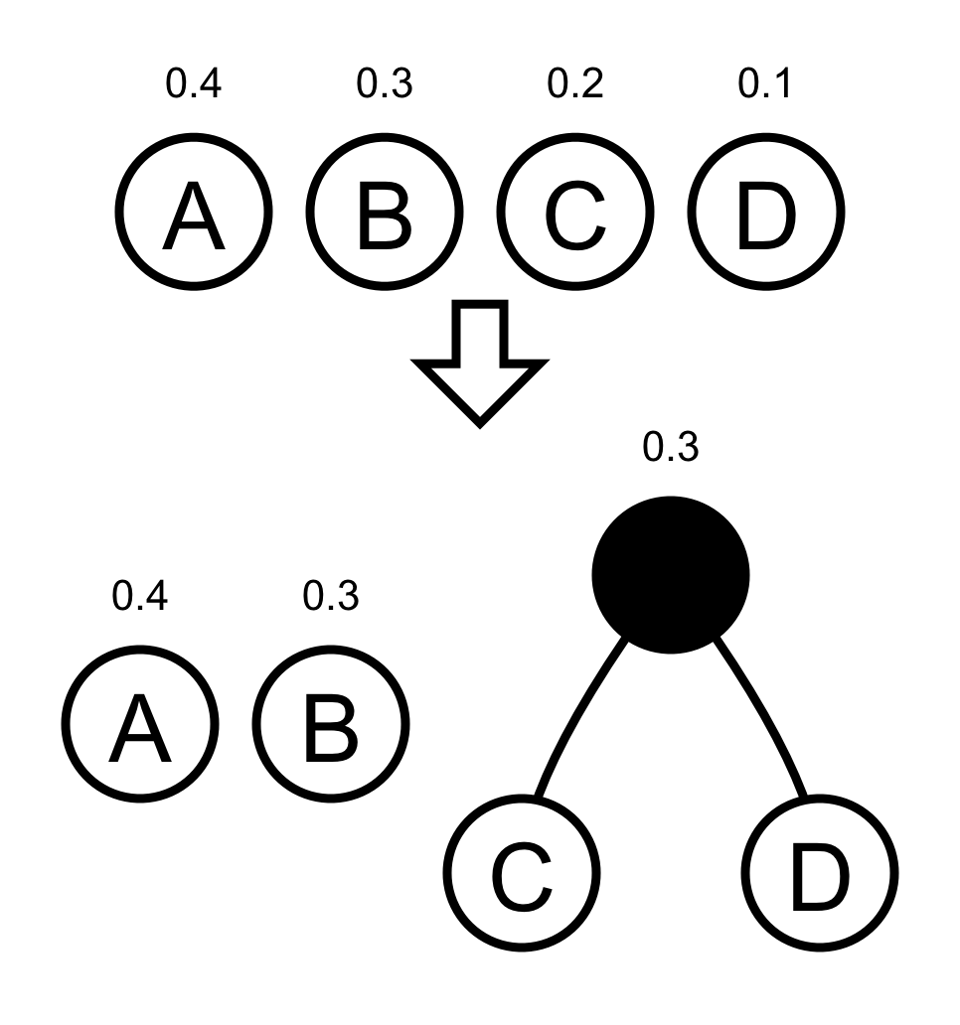
• Repeat until there is only one object left, which is the optimal tree.

Doing a proof of the optimality is out-of-scope here, but it's not too hard.

Back to Distributions

If we squint, the prefix-coding setting is very similar to our problem of generating distributions. Imagine, instead of generating the outcomes from our distribution, we're "given" an object from a distribution which we then have to navigate the tree to, and we want to do so with the least number of hops down the tree. This is, in fact, the same problem as minimizing the expected length of an encoding from an alphabet with assigned frequencies (as this is also measured in hops down the tree).

Given the frequencies, we can build an optimal tree using a priority queue and the following code:

func Distribution[T any](t outcome[T], ts ...outcome[T]) *Sampler[T] {
    h := newHeap[Sampler[T]]()
    h.push(singleton(t.p, t.t), t.p)
    for _, t := range ts {
        h.push(singleton(t.p, t.t), t.p)
    }

    for {
        a, aw, _ := h.pop()
        if b, bw, ok := h.pop(); ok {
            h.push(choice(&a, &b), aw+bw)
        } else {
            return &a
        }
    }
}

This is not quite the same as the approach described in Keith's post, since we never stop at an interior node while in Keith's, he does. But I think it's a lot simpler to implement and only requires O(nlogn) time rather than O(n^2)!