Chapters 1 & 2 of Feedback Control

Hello! I hope you all had a good weekend. This is the first "study group" issue where I will share thoughts on the first two chapters of Feedback Control for Computer Systems: Introducing Control Theory to Enterprise Programmers.
As a reminder, two weeks from now we will talk about the next two chapters. I'd like to have a diverse set of viewpoints on this stuff so even if you did not reach out for this issue please consider sharing your thoughts on those!
For more real-time discussion, please see the NULL BITMAP Discord.
For more background on the topic and why we're discussing it, I wrote this earlier post. It covers the basics of what kind of problems we are interested in solving and why I think it, in general, should be of interest to people who are into databases.
The first two chapters of the book are pretty high-level but they go into some specific examples that I think are illuminating.
Chapter 1
I think the first thing that this book goes through that was interesting to me is regarding how to think about a problem through the lens of feedback: lots of presentations I've seen either treat the problem completely abstractly or start from a problem that seems tailor-made to this kind of analysis. By comparison, I think this problem seems fairly realistic, it's just a pipeline and we're just trying to keep the queues at a reasonable level.
We derive from first principles the idea that the only hope we have of solving this problem is to base our policy off of the true, observed behaviour of the system. There's simply too much randomness involved (and in fact, modeling this as randomness dispenses any notion that we could control for it all) for anything else to work.
We first derive what we will later know by the name of a P Controller, where we choose our input setting proportional to the difference between the desired output and the true output.
I copied over his code and added some matplotlib to plot the results. Note that there's a couple typos in the code in the book, at least in my copy. There's a working version on the author's GitHub. My output looks pretty much the same as his:
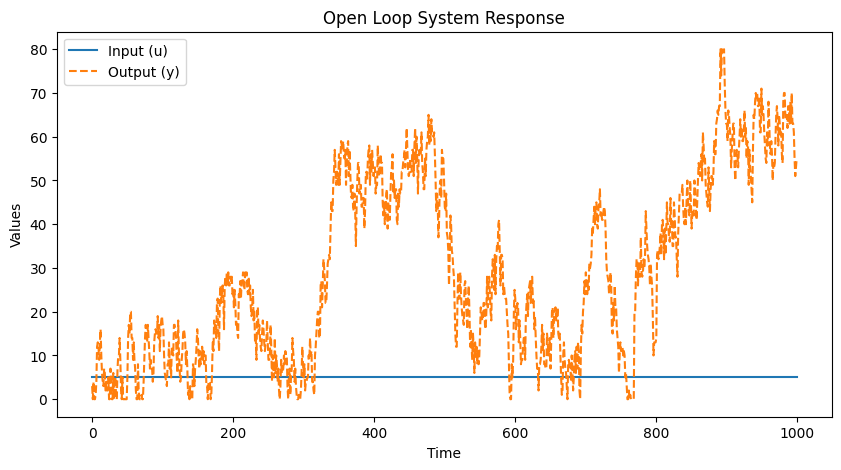
If you've never gotten a handle on using Jupyter (or editing notebooks in VS Code) I recommend it, it's fun to cosplay as being a data scientist if that's not something you do every day and it's fun and visceral to get really quick turnaround on your experiments.
Chapter 2
Chapter 1 rederives the need for control from first principles as a way to convince you that this is a thing worthy of study. Once you're there, chapter 2 hits you right off the bat with the thesis of the book, which is the value of the feedback principle:
Continually compare the actual output to its desired reference value; then apply a change to the system inputs that counteracts any deviation of the actual output from the reference.
There is a really great insight a little later, which is that the goal is never to completely eliminate the error with a single step; doing that would require a fully understanding and model of the system, of course! But as long as we are able to make a step in the right direction, over time, we can make many such steps that will, over time, eliminate the error.
Two more insights I thought were really great were in the setpoint section.
First, the observation that control is a different beast from optimization. We are not concerned here with finding the optimal value for some function, although maybe you could cast it that way in some circumstances. From the perspective of control we must always have a setpoint which we are trying to match, we can't just point a control system at a problem and have it spit out this value. This might sound obvious, but we might want to, say, frame a problem as "give me the size of this cache that gives the fastest response time." No, you need to be tracking some real signal that you are trying to control. This generally means we're controlling something with two ends of a tradeoff that we have some external opinion on ("I would like my cache hit rate to be 95%").
The second observation (and this is the one that sold me on this book in the first place), is the idea that the signal must be able to straddle the setpoint. I encountered this when I was trying to control a queuing system (before I had heard of this book). I thought, "well, I'd like to keep the queue empty, so that should be my target." But this doesn't work for control, because the queue length can never be smaller than zero, and so we can only ever generate any kind of pressure on the signal in one direction. The fact that this book was aware of a big problem that I had encountered when I didn't know anything at all convinced me that we would be solving real problems I had.
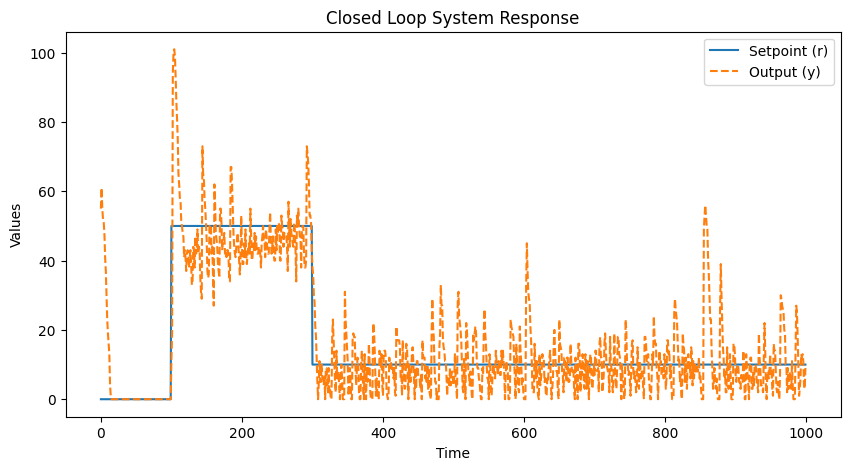
Here is a Jupyter-able version of the code from this chapter, which tracks a cache hit rate. I modified it a bit to mess with the different values of k:
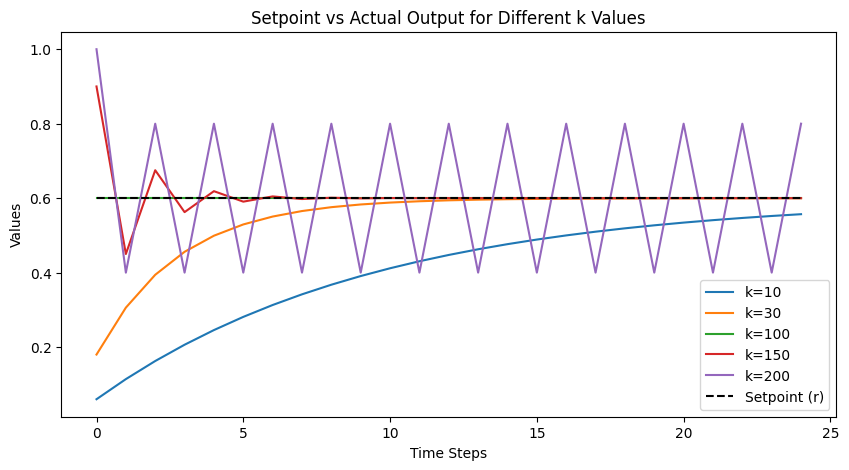
I think one way to view these two chapters from a technical communication perspective is that chapter 1 is bottom-up: we start from a problem and derive how to solve that problem arriving at feedback. Chapter 2 is more top-down: we start from the premise of control and see where that leads us.
Commentary
Only received a bit of commentary on these chapters, which is expected because this was just an introduction to the problem space, and we haven't really gotten into the meat of problem-solving. I got a couple, though:
Ilia wrote:
i guess it's interesting how the first couple of chapters are foreshadowing the concept of the PID, in that (P) you need a target and therefore you will have error from the target that needs addressing, which is the job of a P term, (I) you may end up consistently missing the target by fearing overshooting with just a P controller, so you also use an I term to respond more aggressively to persistent error, (D) if you start overshooting and oscillating and threatening to destabilize then you can monitor the increasingly large changes with a D term and force the controller to calm down
Another friend wrote in to say he'd experienced a somewhat similar problem that felt like rate limiting: he had two "classes" of request that were each entitled to some percentage of capacity, but if one wasn't using all of its capacity then the other should get to use it. An interesting problem!
Add a comment: