Certificates and Duality


I wanna talk about optimization. Not query optimization, or program optimization, today, but the other kind. Mathematical optimization. Like when your high school math teacher told you to find the maximal values of -72 + 66 x + 13 x^2 - 6 x^3 - x^4. Questions like, in this graph:
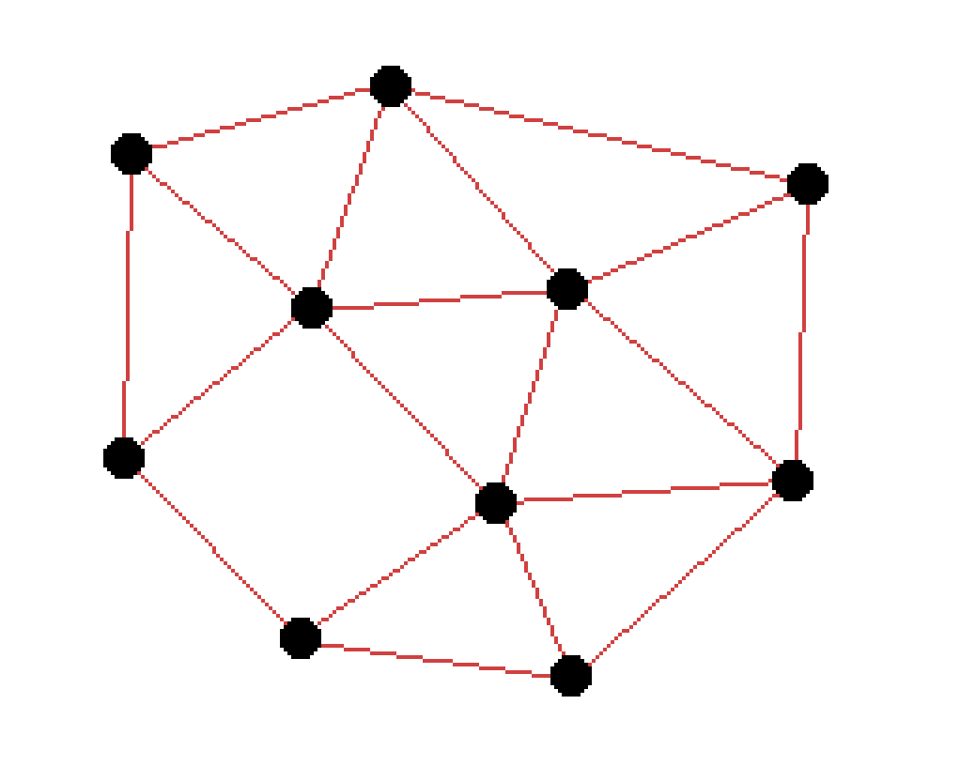
Find a set of vertices that touches every edge. Such a set is called a "vertex cover." One valid vertex cover is:
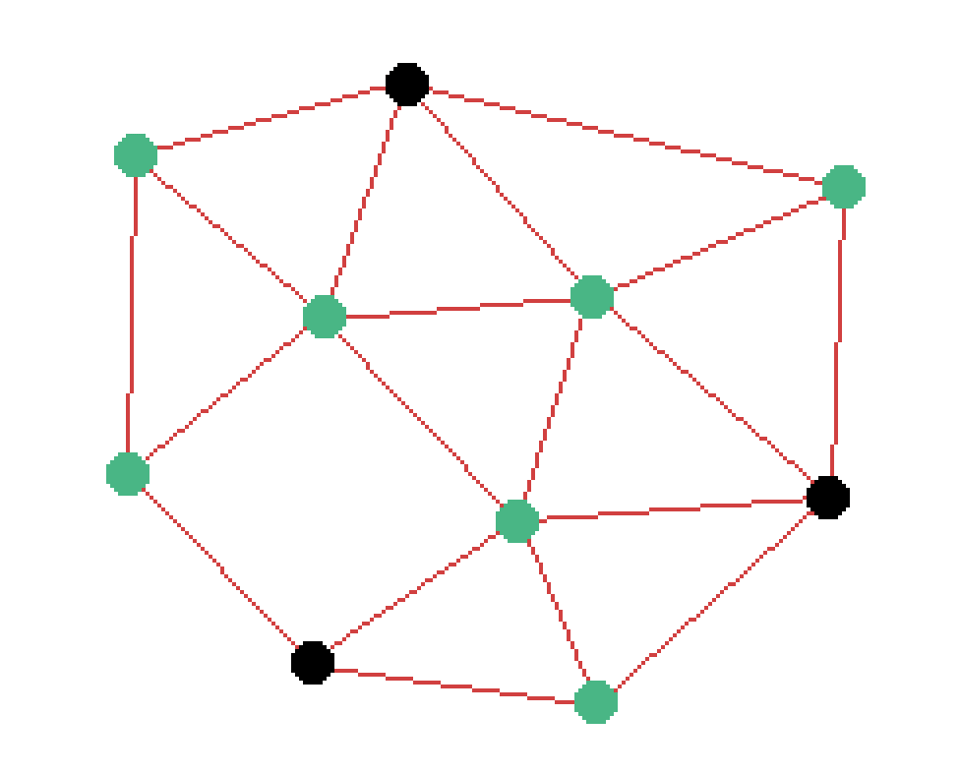
So then the optimization problem is to find the smallest vertex cover possible.
This is the crux of "combinatorial optimization." But what's that all about? Like, what's the stuff that, if you got into it, you'd find yourself saying, "god dang, these people are really into _____."? And, well, there's a couple of those things, probably. But one of them, I think, is the idea of a certificate.
As a programmer, it's easy to look at "optimization" as a "process," something you plug an object into and get a better version of it out. This is kind of at odds with the mathematical understanding, which is that "optimality" is a binary property of a solution to a problem. It's ungrammatical for something to be "more optimal" than something else. Something is either optimal or it isn't (not to say this field isn't also interested in approximate solutions to problems).
In particular, we're very interested in what kind of guarantees we can get about solutions to problems. If we can't be guaranteed that a given solution is optimal, it would be good to have some kind of bound on how far off it might be. That is, if I hand you a problem, and you give me back a solution, I'm not just interested in a raw solution, I also want some kind of evidence that that solution is good. Maybe if not optimal, but not too far off. How can we do that?
This is where another classic tool in optimization, called duality comes in. Often, optimization problems have a kind of opposite "friend," called their "dual," which is related to them in an important way. The dual of the vertex cover problem is the maximum matching problem. Finding the largest set of edges in a graph that do not share any vertices:
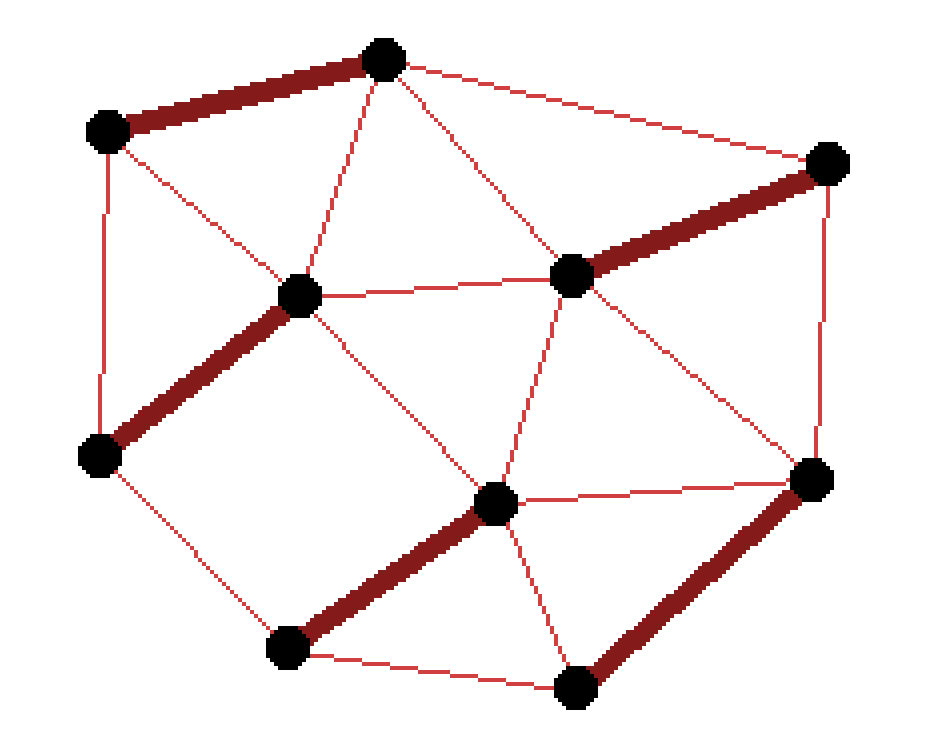
Note some obvious symmetry between the two: vertex cover is a minimization problem, while maximum matching is a maximization problem. We can always find a vertex cover by taking everything (but we then hope to make it smaller), we can always find a matching by taking nothing (but we then hope to make it bigger).
The cool thing is that the minimum vertex cover and maximum matching problems on a graph exhibit what is called weak duality: every solution to maximum matching is no larger than every solution to vertex cover.
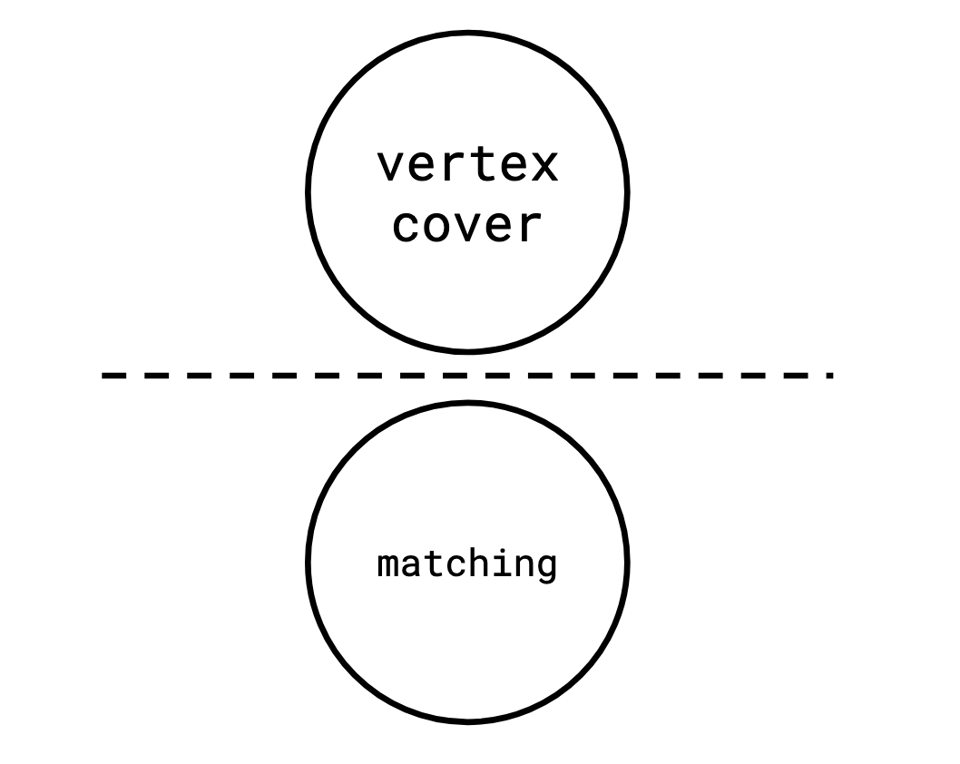
This gives us some useful tools: because we were able to find a matching of size 5 in our graph, we know that there can be no vertex cover smaller than that.
With some problems, we are particularly lucky, and these two zones of solutions kiss each other in exactly one place: the optimal solution to each:
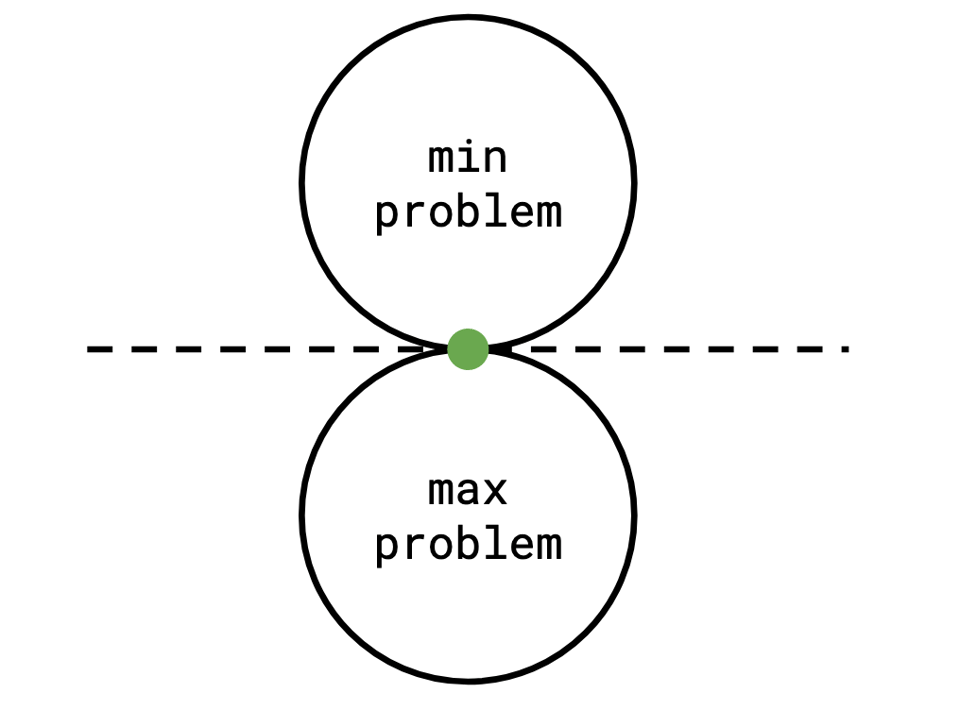
Problems like this, when the optimal solutions meet, are said to exhibit strong duality.
In the case of a bipartite graph, in fact, min vertex cover and maximum matching actually do exhibit strong duality (This is König's Theorem)!
This is great if you are interested in convincing people that your solution is optimal: simply provide a solution to both problems which have the same value, which is irrefutable evidence that no better solution can exist.
This stuff comes up...a bit, in query optimization. At least, I think the high level ideas are relevant to important modes of thinking. But mostly I think this stuff is fun. If you are interested in this kind of stuff my recommendation is In Pursuit of the Traveling Salesman by Bill Cook. This will not be our last foray into combinatorial optimization at NULL BITMAP.
NULL BITMAP is free. If you earn a software engineering salary and think you've gotten some value out of these posts, please consider tossing a couple dollars to the Palestine Children's Relief Fund.
