Bloom Filter Sizing

Here's a question: say I have two streams of objects I want to construct Bloom filters over, one stream is red and one stream is blue and they're about the same size. I have two options:

1. create a red Bloom filter and a blue Bloom filter, and route all of the messages which are red to the red filter and route all of the messages which are blue to the blue filter, or
2. create one big bloom filter and for red messages, insert "red:"+key and for blue messages, insert "blue:"+key.

Which is better? Better strictly in the sense of "false-positive-rate vs. memory tradeoff."

My intuition was that option 2 was better, because every individual bit has more freedom of where it can live, even if there are more bits sharing that larger space, but there's a similar argument that maybe option 1 might be better because now red and blue can collide when they couldn't before.

However, the answer is that both alternatives are about the same.

This becomes obvious if we squint at the formula that approximates the false-positive rate (n is the number of elements, m is the number of bits, k is the number of hash functions):

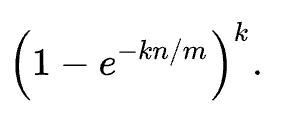
The n/m suggests that doubling the number of elements and doubling the amount of memory available will result in a comparable false-positive rate, which means that the number of false positives experienced collectively by our red and blue Bloom filters will be about the same as our big filter.

This is not the most satisfying explanation, though, it doesn't really give any intuition for why both of these approaches are the same, so lets explore that a bit.

One easy observation is that we can turn an option 2 setup into an option 1 setup quite easily:

• take your N bytes of memory that you'd be using for your big bloom filter and split it up into two N/2-byte bloom filters.
• for every object you have, compute an additional hash function that outputs either red or blue, and store the object in the corresponding bloom filter.

Now we've recreated option 1 from option 2: we have "red" objects and "blue" objects and they each go in their own filter. This more or less shows that it's impossible for option 1 to have a better false positive rate than option 2. If it did, well, we could make our bloom filters arbitrarily better by continually bifurcating them (at least until they hit a single bit).

That's kind of nice! But it doesn't refute my original intuition and I don't see an easy way to make the same kind of argument in the reverse direction. It does kind of give a hint to the structure of what is going on here, though:

Every hash function we compute for a Bloom filter looks like a series of bits (we'll compute several of these for a given object, and use them to index bits in the Bloom filter):

11011001

We can visualize the indices in an array as a tree where we find a given index by repeatedly splitting the array in half: a 1 puts us in the right half of the array, a 0 in the left half:

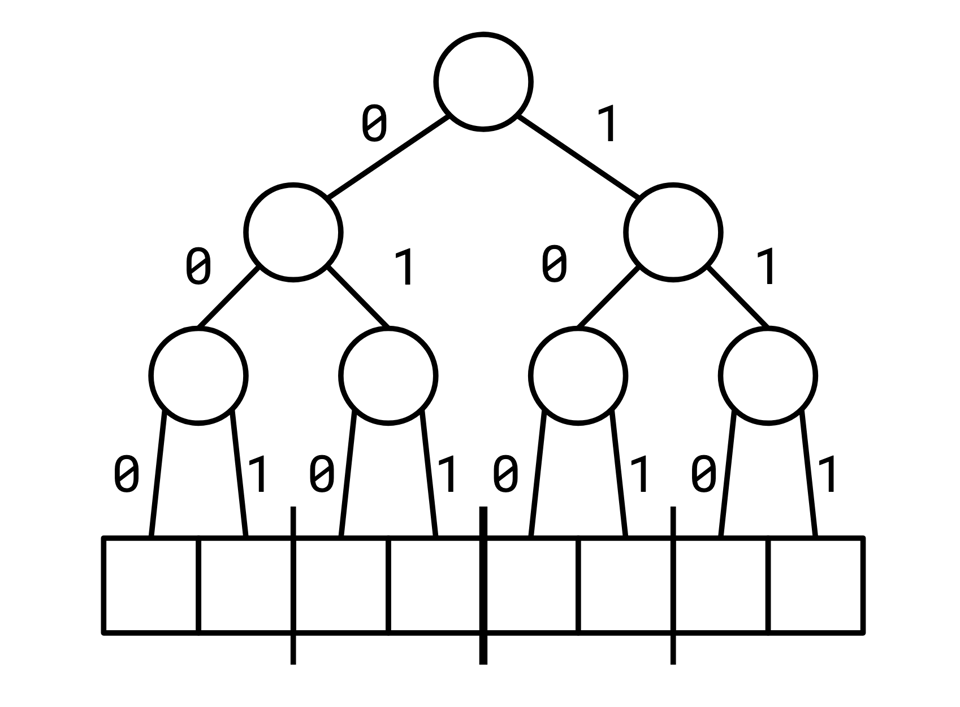
Viewed this way, splitting our Bloom filter memory into two could be seen as fixing a bit at the beginning of each of our hash functions. All of our red values are 0... and all of our blue values are 1...

This isn't quite equivalent to the distinction between option 1 and option 2, because in option 2, the bits corresponding to a given object can straddle different parts of the address space: a key could have a bit starting with 0 and a bit starting with 1.

It does give some intuition for why they aren't vastly different though: both options get to shove an extra bit into each of their indexing: option 1 does it by remembering whether a key was red or blue, and option 2 does it by giving each key twice as much space (and is thus able to use a single extra bit of addressing).

This doesn't mean the two choices are completely indistinguishable in all cases. We assumed that both sets are about the same size here, but if there's a lot of skew, or the potential for a lot of skew, we might prefer option 2 because it means out bigger set will be spread out across the whole space instead of just one half.

Anyway, for me this was a relief: I didn't want to have to explore de-partitioning my bloom filters if things worked out differently (because partitioning them across threads is a lot simpler than synchronizing access to a big bloom filter, if your data is already partitioned).