Adventures in Probability

I hope everyone had a good weekend. I went on a hike. It was great.

Statistics

One of my great school regrets, next to “taking three years of business classes,” is taking less statistics than I did, which was basically the bare minimum. It was, in fact the bare minimum: one probability class and one statistics class.

In my defense, my probability class was miserable but for a very stupid reason, which was that my professor projected video of himself writing on a piece of paper before a very large auditorium, and that guy was left-handed, and so his hand would cover his notes for like the entire time and it was impossible to see what he was writing. I only figured out that this was why it was so unpleasant like halfway through the class.

One day he started class like "you know guys, my cousin called me last night. And he was laughing, and he said, 'cousin, what are you doing to these kids!'... Guys! I am not a bad guy!"

Anyway. I learned later in life that the fact that I’m terrified of uncertainty is a reason in favour of understanding probability and statistics better, rather than a reason to avoid them. This has led to me doing the computer guy thing of learning about things that everyone else already knew and talking about them like I discovered them.

One thing you learn pretty quick if you look into queueing theory stuff, or control theory stuff, or any kind of performance modeling stuff, is the unreasonable ubiquity of the exponential distribution. That thing shows up all the dang time man. And it honestly took me a bit of meandering around various books and discussions with friends before I really built up the kind of intuition for it that made me appreciate it. Because I think it sort of is one of those things that's like, you have to steep in it for a while before it really sinks in that this thing is extremely foundational and useful. At least that was my experience.

Queueing

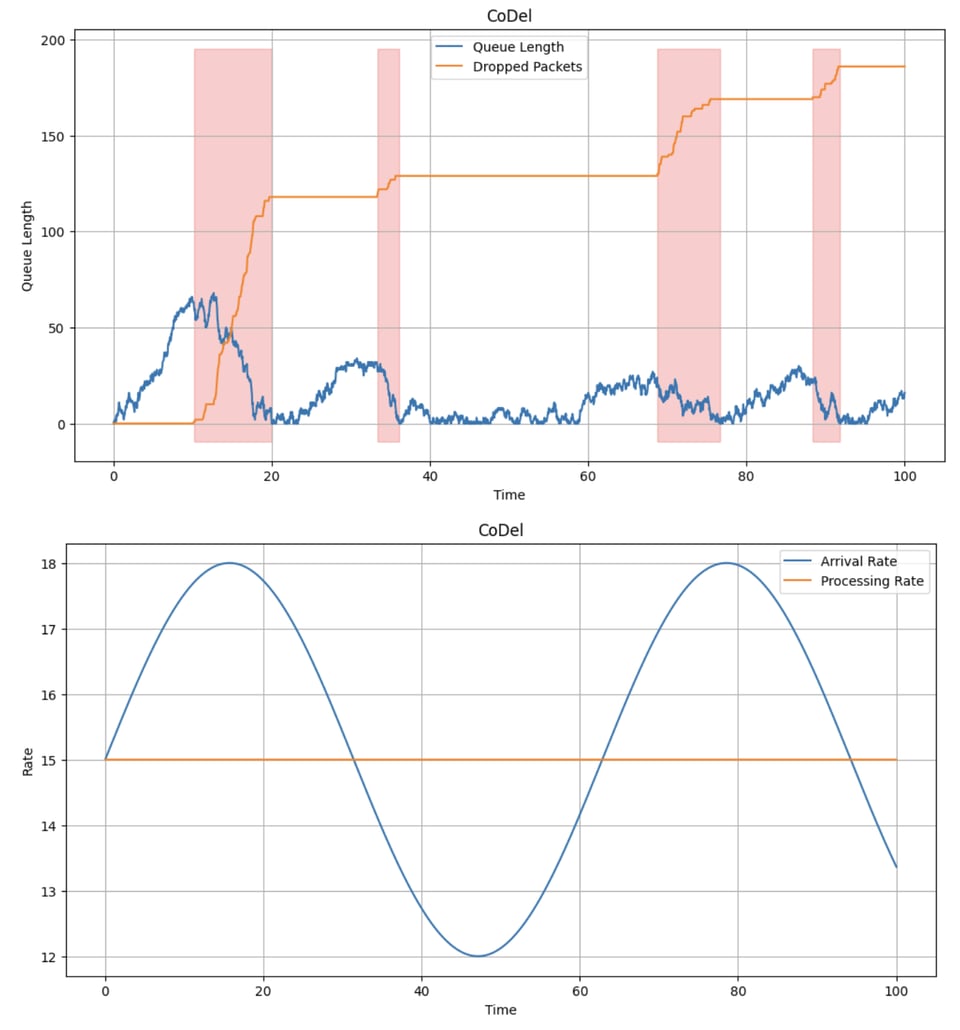
A couple coworkers told me about the algorithm CoDel, which is an algorithm for queue management designed for use in networking. I know little enough about networking that I won't pretend to actually understand the context explained in that RFC (though I only spent a train ride or two going through it). The crux of the algorithm is:

def enqueue(msg):
  if the_queue_has_been_empty_recently():
    timeout = LONG_TIMEOUT
  else:
    timeout = SHORT_TIMEOUT
  enqueue_with_timeout(msg, timeout)

The RFC gives a bunch of justification for why this might be a good way to do this kind of thing; that is a NULL BITMAP for another day. Today's is not really about that (if you are an expert in such things and want to explain it to me please reach out), but about how I have come around to feeling confident in my ability to simulate this kind of thing.

A Poisson point process is a way of generating events along a timeline with some specific properties that we don't have the space to get into here. It’s parameterized by a rate represented by lambda which corresponds to the expected number of events per unit of time.

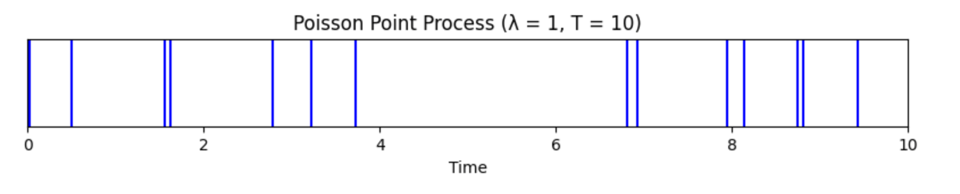
The intuition is that all of the events occur independently of each other, and they never occur at exactly the same time. This is often used to model things like "arrivals of customers at the grocery store," where the arrival of one customer has no bearing on the arrival of another one. Perhaps that's not true in reality, but it makes the model work.

The important connection to the exponential distribution is that the amount of time in-between any two successive events is an exponentially distributed random variable. This means we can simulate it like this:

T = 10
rate = 1
t = 0
events = []
while t <= T:
    t += np.random.exponential(1 / rate)
    events.append(t)

We can interpret this as the points in time that events arrive at a system.

It's also common (more for convenience, than realism) to treat the time it takes to service an event in a queueing system as exponentially distributed. If we only work on one job at a time, that means job “completions” also follow a poisson point process: they’re discrete events separated by a time sampled from the exponential distribution.

We might think, then, that we have a simple way to model the system overall: model two poisson processes, one for the job arrivals with rate λ, which increments the queue size by one (capping at the maximum size of the queue), and one for job completions with rate μ, which decrements the queue size by one (capping at 0). So we can simulate them both at the same time and walk over their events in lockstep to run our simulation:

T = 10

arrival_rate = 1
t = 0
arrival_events = []
while t <= T:
  t += np.random.exponential(1 / arrival_rate)
  arrival_events.append({"t": t, "kind": "arrival"})

completion_rate = 2
t = 0
completion_events = []
while t <= T:
  t += np.random.exponential(1 / completion_rate)
  completion_events.append({"t": t, "kind": "completion"})

events = sorted(arrival_events + completion_events, key=lambda x: x["t"])

for event in events:
  # ... process the event ...

This does work, but it turns out that due to some nice properties of these distributions, there’s an even simpler way.

If we overlay two PPPs, one with blue events, and rate λ, and one with red events with rate μ, here's what that might look like, with λ = 1, μ = 2:

An amazing fact is that if we put on our colourblind glasses, the result is indistinguishable from a single PPP with rate λ+μ:

And then, any particular event will be blue with probability λ/(λ+μ) and red with probability μ/(λ+μ) (it's proportional, it's like, weighted by the rate). So when we observe any particular event, we can decide on-the-fly which kind of event it was. This means we can actually simulate a process like this in the following way:

T = 10
arrival_rate = 1
completion_rate = 2
t = 0
events = []
while t <= T:
  t += np.random.exponential(1 / (arrival_rate+completion_rate))
  if np.random.uniform() < arrival_rate / (arrival_rate+completion_rate):
    event_type = "arrival"
  else:
    event_type = "completion"
  # ... process the event ...

These distributions freely combine and separate proportional to their rates. I can take a hunk of rate three and a hunk of rate five and smash them together to get a hunk of rate eight. Or yank them apart to get a pair of rates two and six.

This can be used for lots of great things. If I have a load generator for a system that generates events with delays uniformly at random, I can’t easily split that into two load generators with half the demands, since the resulting distributions don’t match. If I generate events in this way, though, I can.

Maybe best of all, it's good for simulating the kinds of systems you might find in a queueing theory textbook.

Anyway, here is the simulation I ended up doing:

Statistics Class

They always drive home that it’s important that the exponential distribution has the “memoryless” property: that if you wait t seconds for an event, and no event comes, the expected time to the next event is exactly as it was before you waited. The exponential distribution is the only continuous distribution with this property.

I always thought this framing was weird. Why are we making such a big deal and giving such a goofy name to this property when it’s just describing one kind of distribution? Aren’t properties like this useful to the extent that they can be treated abstractly and not depend on the underlying object?

I think if I were in charge of presenting this material to students I'd do it by introducing the concept of memorylessness and by showing how good memorylessness is, how many wonderful things you can do with it. And then one day I'd be like, "well, it sure would be nice if we had any distributions like that!" and then whirl around with my piece of chalk to deliver the exciting news that we do. Exactly one, in fact.

I'm not sure who this post was for. If you already know this stuff you're probably like "yeah...duh," and if you're at the place where I was before I started tinkering with it this might not have convinced you how great it is. I don’t know a way to communicate it that doesn’t go through a lot of simmering in the exponential distribution and its applications. If only that guy had been right-handed I might have understood this sooner.