A Left-to-Right Mental Model for Datalog

Note: see the end of this post for some housekeeping on last week.

I get the sense that datalog scares a lot of people off. And I get that people might not be all that persuaded by the argument that datalog is one of the most natural query languages you could dream up and has compelling interpretations in first order logic and model theory and all kinds of other great stuff [1].

But one of the nice things about having a thing like a query language that has that kind of natural construction is that there's a lot of different ways to think about how it works, and if one doesn't make sense to you there might be another one that does.

Here's one that I find helpful in some contexts (but not others). It's a very algorithmic model that maps very cleanly onto, in particular, bottom-up approaches for evaluating datalog. You can use this pretty much directly to compile datalog into a dataflow graph.

The first thing that made me really understand datalog was to think of a datalog "query" as a problem that has a solution, rather than a query that has a result. Logic people call these solutions "models." Evaluating a datalog query is thus solving this problem. There are interpretations of datalog that lean more or less into that, but you can think of what we're talking about today as like, describing a procedure that finds that solution (there are other ways that define it more declaratively).

First of all, datalog has tables just like SQL: sets of rows. Very importantly, unlike SQL, these are actually sets. Trying to add a tuple that already exists to a relation is a no-op.

We start with some set of tables and rows that live in them. For whatever reason this is called the "edb" of a datalog program.

We create a table with rows like so. This creates two tables named Animal and Country. Columns don't have names in datalog.

Animal("Sissel", "CA").
Animal("Smudge", "CA").
Animal("Petee", "US").
Country("CA", "Canada").
Country("US", "United States").

You can just think of a term like Animal("Sissel", "CA") as a struct, or a row, or something. It's just some compound data.

In addition to those starting rows, we have rules for producing new rows.

We might have another table "name" that just contains every name in the system.

Animal(X, _) -> Name(X).
Country(_, X) -> Name(X).

Usually these rules are written the other way around, but in the particular mental model I want to highlight here I think it makes more sense to write them this way. In Animal(X, _) -> Name(X), data flows from Animal into Name.

We'd see the row Animal("Sissel", "Canada") and that would match on the rule Animal(X, _) and produce a new row Name("Sissel"). And so on for the other rows in the system. That's the core of the idea: you have a graph of all these tables, and then the rules are the edges between them that let them populate each other.

You do filters by just specifying the values of particular columns:

Animal(X, "Canada") -> CanadaNames(X).

Writing multiple tables on the left side does a join between them:

Animal(AnimalName, CountryCode),
Country(CountryCode, CountryName)
  -> AnimalCodes(AnimalName, CountryName).

This constructs a new table called AnimalCodes.

This juxtaposition of two inputs being a join is fairly natural if you think of this as a pattern match. You just try every possible pair of rows, and the ones that match produce a new row.

In SQL, this would be something like:

SELECT animal_name, country_code
  FROM animal, country
 WHERE animal.country_name = country.country_name

And that's it: you know datalog. You take one of these and keep applying rules until you can't any more (of course, there are some smarter approaches to scheduling such things), and the resulting set of tables is the evaluated datalog program.

There is one other big difference from SQL which is that since SQL is inherently tree-structured, it doesn't syntactically let you express that some of these rules should be cyclic. Datalog has no such restriction. This means you can express things like graph reachability (which are not expressible in SQL without recursive CTEs):

Edges(A, B), Reachable(A) -> Reachable(B).

Data flows from edges and reachable back into reachable. Turning this into a dataflow graph, it might look something like this:

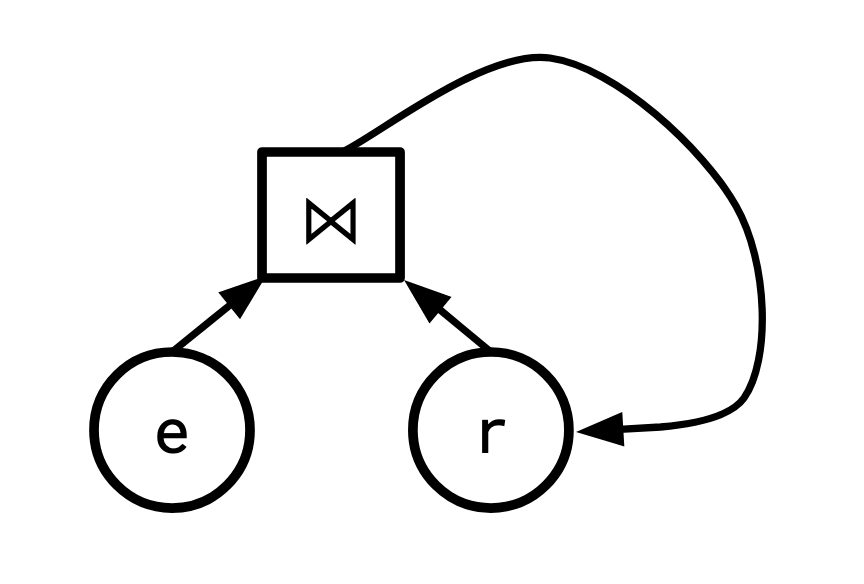
This is sort of why datalog comes up a lot in the discussion of dataflow systems, if you write the datalog rules like this, with the conditions on the left and the result on the right, it's sort of just a DSL for directly writing out dataflow graphs. But I don't think that's necessarily obvious from the usual presentations.

[1] See the Alice Book for more of that. They (more or less) call this the fixpoint interpretation.

Update on Last Week

Last week we talked about a surprising behaviour of scoping and aggregates in SQL:

> CREATE TABLE aa (a INT);
> INSERT INTO aa VALUES (1), (2), (3);
> CREATE TABLE xx (x INT);
> INSERT INTO xx VALUES (10), (20), (30);

> SELECT (SELECT sum(a) FROM xx LIMIT 1) FROM aa;
6

Julian Hyde pointed out that BigQuery actually returns 3 6 9. The correct answer, according to the SQL spec, is 6:

A couple people (thank you Lukas Eder, Julian Hyde, Alex Miller, and Brian S O'Neill!) helped me try this query out on a couple of different databases, it turns out not all of them answer it correctly! Here's a summary of the results:

Answer the Query Correctly (6)

• CockroachDB
• MariaDB
• MySQL
• Sqlite
• Postgres
• SQL Server
• DuckDB
• Firebird
• HANA
• YugabyteDB
• HSQLDB
• DB2

Answer the Query Incorrectly (3 6 9)

• Oracle (!!)
• Derby
• BigQuery
• H2

Unable to Run The Query As Written

(Though it's not impossible that there's some way we could massage the query to give a meaningful answer.)

• Informix
• EXASOL
• SingleStore
• Trino
• Vertica
• Snowflake

If you have access to any other databases (or are able to resolve whatever issues blocking the "unable to run" ones are having) I'd be curious to learn more about what the results are here, please reach out.