Performance of NIST DRBGs
Hello! Welcome to another Illuminated Security newsletter. This week I'm going to tell you a bit about secure random number generation with some benchmarks and pretty graphs.
Cryptography essentially relies on random values. Cryptographic keys must be generated with sufficient entropy to make them hard to guess. But it doesn't end there, because secure encryption and signature algorithms often require the injection of per-message randomness in the form of nonces (numbers-used-once). In this newsletter I'll talk a little bit about how this is done, look at NIST's recommendations in particular, and examine the performance of these compared to alternatives.
PRNGs
A lot can and has been written about how to generate these random values, but in many cases the right answer is to read them from a cryptographically-secure pseudorandom number generator (CSPRNG). On Linux this typically means reading from /dev/urandom or /dev/random or using the getrandom(2) system call.
The implementation of a CSPRNG in the kernel typically mixes a bunch of different entropy sources, such as hardware PRNGs (like Intel's RDRAND CPU instruction), and unpredictable system measurements like the timing of user keystrokes. Readings from these entropy sources are usually pushed into a cryptographic hash function to mix them together securely. In Linux, this is done using Blake2s.
This short but high-entropy hash output is then fed into a stream cipher to expand it into a longer sequence of bytes. Looking at Linux again, this uses the ChaCha stream cipher.
This two-phase process is similar to key derivation using HKDF: first we extract some uniform random bytes from entropy sources, and then we expand those bytes into lots of key material. Unlike HKDF, however, a CSPRNG is not deterministic: additional entropy is periodically re-injected into the process so that the output is (eventually) unpredictable even to an attacker that captures the entire internal state at some point in time. There are some other details I'm glossing over here, but that gives you a decent intuition for how these things work in practice.
NIST's recommendations
NIST (the US National Institute of Standards and Technology) publishes standards for creating CSPRNGs for use in US federal systems. These standards come in three parts:
SP 800-90A defines what NIST calls Deterministic Random Bit Generators (DRBGs). These primarily serve the same purpose as the stream cipher in the Linux kernel design: expanding a small high-entropy input into a larger sequence of random bytes. However, the same spec also covers seeding and periodic reseeding from entropy sources (the extract phase).
SP 800-90B describes the requirements for entropy sources and various statistical tests for measuring the entropy of those sources.
Finally, SP 800-90C brings the two together and describes approved methods for combining a DRBG and entropy sources to create a CSPRNG (which NIST calls an RBG for Random Bit Generator).
In this newsletter I'm just interested in the first of these documents about the DRBGs, their design and relative performance.
Approved DRBGs
SP 800-90A defines three approved DRBG designs. It used to define a fourth but we don't talk about that one... (Actually, people do talk about it, and they should. But that's not what this newsletter is about). The three current approved designs are:
Hash_DRBG is based on using a cryptographic hash function such as SHA-256. The expand phase effectively runs the hash function in randomized CTR mode (without a key), and then there is a bunch of other (quite complex) stuff that happens to generate the next state and incorporate any fresh seed material and other inputs.
HMAC_DRBG is probably the most sane design on paper. It generates output bytes by using HMAC in something like output feedback mode (OFB). It's not far off what HKDF does, but with a bit more complexity in how it mixes in fresh seed data from entropy sources.
Finally, CTR_DRBG eschews hash functions entirely in favour of using a block cipher like AES in CTR mode. This is great for the expand phase, in theory providing similar performance to ChaCha. However, it's a bit weird to then also use the block cipher for mixing in fresh entropy, which is really what hash functions are for. The design also involves changing the key regularly, which is quite expensive in AES.
To my eyes, all of these designs have some quirks and inefficiencies, but none of them look obviously broken.
Backtracking and prediction resistance
NIST defines two security properties that DRBGs should exhibit:
Backtracking resistance means that if an attacker somehow captures the entire internal state of the PRNG at a point in time, they are unable to determine any outputs of the PRNG before that time. This property is referred to as forward secrecy in cryptographic protocols, and in the case of PRNGs it is achieved by overwriting the internal state as part of every operation. All of the NIST DRBG's achieve this property.
Prediction resistance (PR) is the converse property: an attacker with access to the full state at a point in time will not be able to predict future outputs after that point in time (assuming they don't maintain ongoing access). This is typically achieved by periodic re-seeding with fresh entropy. This is an optional (but strongly recommended) feature, to accommodate PRNGs that don't have ongoing access to an entropy source. In practice, the PRNG will typically automatically reseed periodically, and may also provide a way to force reseeding before an operation.
Performance comparison
Recent versions of Java provide implementations of all of the NIST DRBG designs as part of the SecureRandom framework, so I decided to test how they perform relative to each other and other algorithms.
Obviously, this is just one implementation of these algorithms so there may be significant differences when compared to other implementations. However, I've looked at the source code in OpenJDK and the implementations are pretty straightforward and not doing anything daft. I believe we can use these to get a reasonable idea of the relative performance of the designs and some of the strengths and weaknesses of them.
For the test, I instantiated each of the DRBG implementations, ran some warm-up runs to make sure the JIT was compiled, caches filled, etc. For the main test I then read 50MiB of data from each DRBG in chunks of different sizes, from 16 bytes to 4096 bytes (4KiB), to see how the performance changes as you request more data at once.
For HMAC_DRBG and Hash_DRBG I've included numbers for both SHA-256 and SHA-512, as these can have different performance characteristics on different CPU architectures. The machine I ran the tests on is a 64-bit Intel CPU, which favours SHA-512, and you can see that in the results. For CTR_DRBG I initially tested both 128-bit and 256-bit keys, but there was very little difference so I've just plotted the 128-bit results. Java's implementation of CTR_DRBG also lets you specify whether to use a "derivation function" during seed updates (use_df variant in the graphs). I haven't looked in much detail at what this does, but it's clear that it comes with a performance penalty. (As it only makes a difference when PR is enabled, I've not shown the results when it is disabled).
I've tested each DRBG with prediction resistance on (pr_and_reseed) and off (reseed_only). When it is enabled, every call to read bytes from the DRBG results in reseeding the internal state with fresh entropy, whereas with reseed_only it reseeds periodically when the number of calls to get random bytes exceeds a threshold. Java hard-codes this threshold to Integer.MAX_VALUE which is over 2 billion, so is basically disabled. If you want prediction resistance, ask for it! I configured Java to use a non-blocking entropy source in any case.
The tests were carried out on an aging 2.5GHz Quad-Core Intel Core i7 MacBook Pro with 16GB RAM running macOS Monterey 12.6.2 with nothing else running at the time (as far as possible).
Results
The first graph below shows the basic performance results in terms of bytes read per millisecond for each algorithm. The x-axis is the number of bytes read in each call and is log-scale. My intuition before running the tests was that CTR_DRBG would be the fastest algorithm due to the availability of AES-NI hardware acceleration instructions on Intel CPUs (which Java does make use of), and this is indeed pretty good. But it turns out that Hash_DRBG with SHA-512 is often faster.

Another clear result is that prediction resistance comes at a cost. In almost every case, the algorithm with PR turned on is slower than with it turned off. In some cases, this is a considerable difference in performance. CTR_DRBG's optional derivation function comes at a larger cost, however, so I would recommend disabling that if performance is crucial.
The graph also includes plots for Java's other default SecureRandom algorithms: the ancient SHA1PRNG algorithm (which really shouldn't be used any more) and the NativePRNG implementations, which read from /dev/random or /dev/urandom (or a mix of the two, for added fun). On macOS (and recent Linux versions) both of these are non-blocking so we see that their performance is roughly identical.
However, there is a big caveat about those NativePRNG implementations. You may think that this shows that the DRBG algorithms are faster than the native PRNG! But this is misleading. Although Java claims these are "native" PRNGs, they actually internally mix the entropy into a copy of SHA1PRNG... 🤮
We can bypass this "feature" by calling SecureRandom.generateSeed() rather than nextBytes(). This will directly read bytes from the system PRNG device. As shown in the following graph, this is much faster than all of the other options (so long as you configure a non-blocking entropy source!):

Even this is less efficient than it could be because the read is unbuffered. If we compare calling SecureRandom.generateSeed() to just reading from the device directly, both buffered and unbuffered, you can see that the native PRNG can sustain much faster speeds than any of Java's PRNG implementations:

The fastest DRBG implementation, Hash_DRBG with SHA-512 and no prediction resistance, achieved a maximum of about 190kB/ms throughput (190MB/s), whereas reading directly from /dev/urandom can do more than 2.5x that (over 500MB/s).
But most uses of randomness in cryptography aren't requesting 4kB of data at a time. Typically you'd actually be requesting much smaller amounts. For example, a random nonce or IV used in encryption is around 16 bytes, sometimes a bit more sometimes a bit less. Similar amounts would be requested if you were generating identifiers for session cookies or access tokens instead. If we zoom in on the left hand side of the graph, we see a different picture:
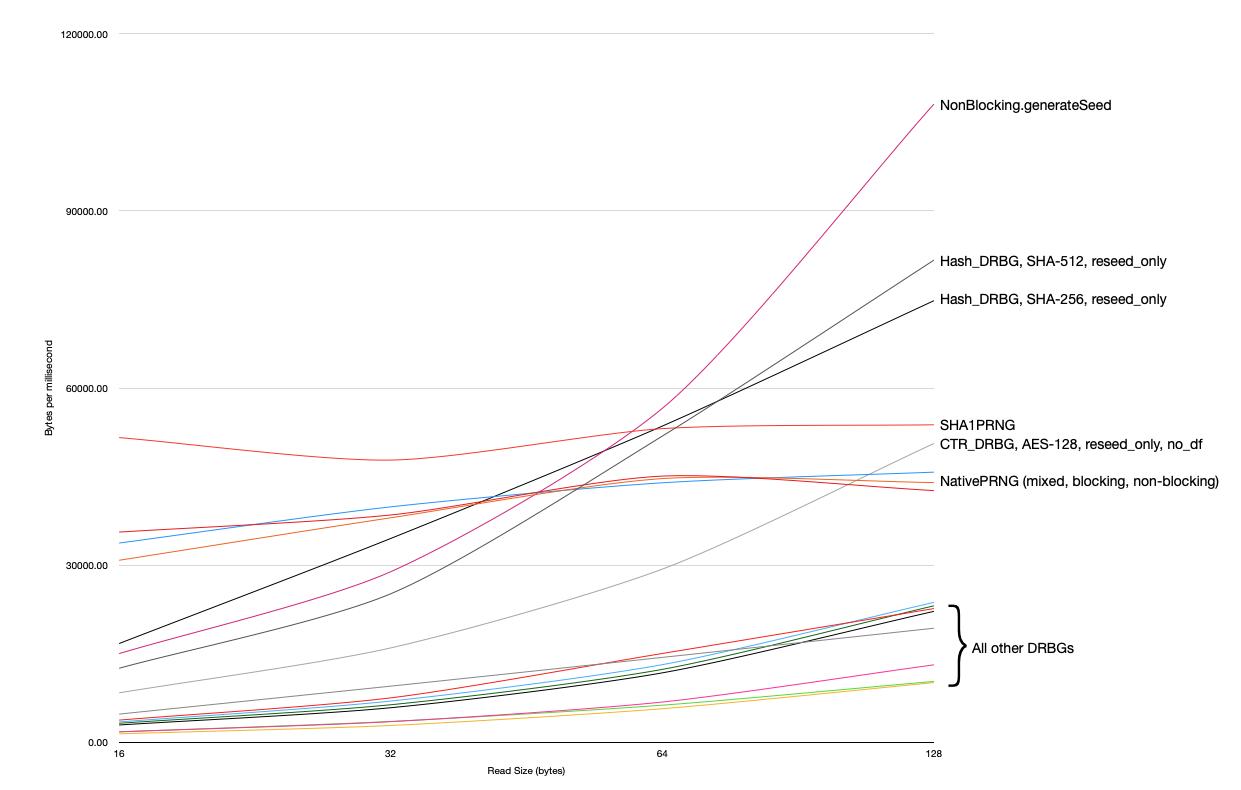
Here we see that the NativePRNG and SHA1PRNG implementations are better at producing many small values than any of the DRBGs. This is because these implementations internally cache a small amount of generated output for a short time (100ms), so are better able to cope with repeated requests for small amount of data. None of the DRBG implementations do this. I can't find anything in the spec that explicitly forbids such caching, but I haven't read every word, so it might be that this is not allowed. Clearly though for the typical many-small-read usage patterns of PRNGs in practice the performance of these DRBGs without caching is dire.
The fastest DRBG implementation for 16-byte reads is Hash_DRBG with SHA-256, which manages to produce data at a rate of around 17MB/s. Per second! This is about a third of the throughput of SHA1PRNG at the same read size, while buffered reads directly to /dev/urandom achieve over 250MB/s—much faster (and can probably still be optimised). To be fair, 17MB/s is fine for a lot of applications—that's over 1 million 16-byte nonces per second. But in the scheme of things it's really pretty slow.
So why are the HMAC_DRBGs so slow?
Most of the DRBGs are pretty slow when requesting small reads of data. You have to read about 40–50 bytes or more before any of them become competitive with the default PRNG algorithms, largely due to the latter's use of caching. Even then, it's only the Hash and CTR DRBGs without prediction resistance that achieve a decent throughput. Prediction resistance causes the PRNG to re-seed after every operation, which involves a lot of additional processing in all of the DRBG designs. It may be better to disable prediction resistance at the DRBG level and instead to manually re-seed the DRBG periodically in application code.
The worst offender by far is HMAC_DRBG. It is much slower than Hash_DRBG, which is surprising because HMAC is just a hash function applied twice, roughly: H(k1 + H(k2 + data)). In the worst case we'd expect this to be roughly half the speed of the raw hash function. But the results show that HMAC_DRBG is much worse than that. In Hash_DRBG, the happy path through the generate code will call the hash function exactly twice. For HMAC_DRBG, however, there will be at least three calls to HMAC, so 6 calls to the hash function. For SHA-512, the results for HMAC_DRBG are approximately 3x slower than Hash_DRBG, so that would make sense. For SHA-256, it can be up to 6x slower though, and the gap for both widens as the data size increases. Whatever the reason for this, it's clear that although HMAC_DRBG appears to be the most robust design it is by far the slowest, never achieving more than about 45MB/s throughput in these tests.
Conclusions
So what can we conclude from all this? Firstly, unless you need to use a NIST-approved PRNG design, there are probably faster options available. Avoiding an in-process DRBG entirely is a good option and going straight to the operating system random device is typically much faster than anything else. Java developers are often advised to avoid SecureRandom.generateSeed() but it is likely both the highest performance and best quality source of randomness. (So long as you are not using a blocking entropy source).
Depending on your threat model, you may also want to consider caching a small amount of random data in a buffer to avoid the overhead of many small reads to the PRNG, regardless of the algorithm.
Of the NIST-specific DRBGs, Hash_DRBG and CTR_DRBG are significantly faster than HMAC_DRBG, with SHA-512 looking like a clear winner on 64-bit machines. Prediction resistance comes with a significant performance penalty, especially for small reads, so consider disabling it and re-seeding the PRNG periodically from application code instead.
Despite its sluggish performance, unless you actually need very high throughput rates, the performance of HMAC_DRBG is likely to be adequate for many uses. In my opinion it is the most robust-looking of the designs: it uses HMAC in a very conventional way, which is not so true of the other options.
Other community news
I was interviewed on the cryptography.fm podcast about Psychic Signatures - the bug in Java's ECDSA signature validation I discovered last year. Check it out and the previous episodes of the podcast, which covers some great topics.
A new draft of Dan Boneh and Victor Shoup's Graduate Course in Applied Cryptography was published. Read the discussion on Reddit.
The next edition of the OAuth Security Workshop will be August 22-24, 2023, Royal Holloway University, London.
If you have any community news about application security or applied cryptography to include in the next edition, or feedback on this newsletter, please email me: neil@illuminated-security.com.
