Rules and Trees
What a week.
I've been consumed for the past few days by CPSC 509, and I can't believe that I even finished it ("finished" might be a bit of a stretch, I do have answers for each question and I hope they're even the tiniest bit correct). I spent last night in a Discord voice channel called "Crying" with two other students taking the course and managed to discuss the homework. If this isn't peak pandemic academia, then I don't know what is.
I still want to continue my habit of writing what I learned in the last week of grad school and talk this week about using inductive rules to define sets. Here's a photo below, rendered in beautiful LaTeX
 When I first saw something like this, I was totally confused. What are those fraction-like things and why do some have tops and why do others have both a top and a bottom? It turns out that that's usually the experience that most people have. That said, it's actually pretty elegant. Let's start with the expressions at the top. We have e is in BoolExp and b is in Bool. This just tells us that in everything that follows, whenever we see the character "e", we can assume that it is a member of the set that we give the name "BoolExp", and whenever we see the character, "b", we can assume that it is a member of the set we call "Bool". Pretty simple so far, right?
When I first saw something like this, I was totally confused. What are those fraction-like things and why do some have tops and why do others have both a top and a bottom? It turns out that that's usually the experience that most people have. That said, it's actually pretty elegant. Let's start with the expressions at the top. We have e is in BoolExp and b is in Bool. This just tells us that in everything that follows, whenever we see the character "e", we can assume that it is a member of the set that we give the name "BoolExp", and whenever we see the character, "b", we can assume that it is a member of the set we call "Bool". Pretty simple so far, right?
We then get into the following
 Let's take a look at the first line. It's just a fancy way of saying "e can be one of: true, false, e and e, e or e". You can extend this definition to get values that "b" can be. Notice that we have some weird recursion going on. Now let's get to the weird fractions!
Let's take a look at the first line. It's just a fancy way of saying "e can be one of: true, false, e and e, e or e". You can extend this definition to get values that "b" can be. Notice that we have some weird recursion going on. Now let's get to the weird fractions!
Take a look at the "fraction" below:
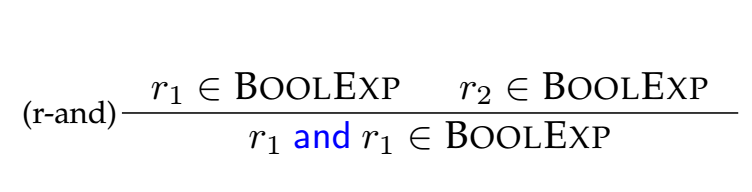 I say "fraction" because that's not the right word for them, but it's something that you can map to. If you look at the "top" part, we have the statement r1 is in BoolExp, and r2 is in BoolExp. This is what we call the premise, r1 and r2 are what we call "meta-variables". If you look at the bottom part, we see that r1 and r2 is in BoolExp. This just says that the meta-variables we declared on the top (the premise) are now used to describe a new member of the set BoolExp, which is r1 and r2. This bottom part is called the conclusion. We now have a name for this "fraction", and we call it a judgement or a rule. The name we give to this rule is "r-and".
I say "fraction" because that's not the right word for them, but it's something that you can map to. If you look at the "top" part, we have the statement r1 is in BoolExp, and r2 is in BoolExp. This is what we call the premise, r1 and r2 are what we call "meta-variables". If you look at the bottom part, we see that r1 and r2 is in BoolExp. This just says that the meta-variables we declared on the top (the premise) are now used to describe a new member of the set BoolExp, which is r1 and r2. This bottom part is called the conclusion. We now have a name for this "fraction", and we call it a judgement or a rule. The name we give to this rule is "r-and".
You can actually do this for every member of the set BoolExp and come up with an equivalent definition for the two-line definition we saw earlier. So why is this useful? It turns out that you can stack these judgements ("fractions") on top of each other to write some cool proofs. They can get so tall or unwieldy sometimes that they're often called "proof trees". Maybe I'll write some more about it another week.
Writing about school aside, this week was pretty eventful personally as well. There was a tweet that blew up about one of my former employers that got a lot of media attention (or as much as a Vancouver tech company can get), which made me introspect about my feelings regarding software and how it's created, deployed, and sold. I haven't had too much time to sit on my thoughts about that for a while so that'll be in another week's writeup.
I also realized again that this grad school thing is hard. There's a lot of ambiguity in most of the things I do. Often I feel like I'm not doing enough, or that I'm somehow behind. I think working with some of my labmates has made me realize that everyone feels like this at some point in school. That said, it doesn't make it any easier to deal with. I'm incredibly lucky that I have people at school who I can talk to that have gone through, or are going through the same thing I am. I guess that's it for this week's writeup.