(No practical ClojureDart tips this issue, only cgrand rambling about drawing lines. Baptiste will be back soon with some FFI experience to share!)

(as usual, all code can be found on GitHub.)

Drawing lines the old way

In the previous issue, young cgrand discovered how to draw circles with cheap integer arithmetic. Now it's time to draw lines!

The intuition I had for circles (using the distance) couldn't apply to lines (or so I thought because I didn't know how to compute the distance from one point to a line at the time).

However what I knew is that if you consider the equation y=ax+b for a line then the value of ax+b-y shifts sign when crossing the line: positive for points below the line, negative for those above. This gives a cheap test to pick which pixel to draw next. Let's call this quantity sf (as "sign flag").

sf(x,y) = ax + b - y

The only remaining question is how to update this value cheaply (multiplication and addition on floating or fixed points a and b).

Before going further we'll restrict the cases to cover by using symmetry: we only consider lines whose slopes a are between 0 and 1 (both inclusive) and we also only consider lines starting at [0 0].

So a and b are not nice integers they are decimals which have to be represented as fixed or floating points. However it's a very math point of view. I only want to draw a segment from [0 0] to [w h] (again, symmetry allows us to assume w >= h and w > 0). So the slope a is h/w and b is 0 since we start at [0 0]. If we substitute it in the formula we want to compute we get:

sf(x,y) = h/w*x - y

which doesn't look like a win with a dreadful division. However we must remember that we only care about the sign of this value and that we assumed w > 0, thus we can multiply the definition of sf by w without changing its sign!

sf(x,y) = h*x - w*y

Given how we restricted ourselves to w > 0 and 0 <= h <= w then we only ever get from pixel [x y] to [x+1 y] or [x+1 y+1] and we start at [0 0] which is perfectly on the line (so signed value we want to compete starts at 0 which means "spot on").

Let's compute sf(x+1,y)-sf(x,y):

sf(x+1,y)-sf(x,y)=
    h*(x+1) - w*y
  - (h*x - w*y)

sf(x+1,y)-sf(x,y)=
    h*(x+1) - h*x 

sf(x+1,y)-sf(x,y) = h 🎉

Wow! quite the simplification! What about sf(x+1,y+1)-sf(x,y)?

sf(x+1,y+1)-sf(x,y)=
    h*(x+1) - w*(y + 1)
  - (h*x - w*y)

sf(x+1,y+1)-sf(x,y)=
    h*(x+1) - w*y - w
  - (h*x - w*y)

sf(x+1,y)-sf(x,y) = h-w 🎉🎉

So we start our accumulator at 0, add h to it, if the result is negative or zero, we go to [x+1 y] else we go to [x+1 y+1] and subtract w from the accumulator.

Let's try!

(defn segment
  "Returns a segment as a collection of integer coordinates from [0 0] to [w h]."
 [w h]
 {:pre [(pos? w) (<= 0 h w)]}
 (->> (iterate (fn [[x y sf]]
                (when (< x w)
                  (let [sf (+ sf h)]
                    (if (pos? sf)
                      [(inc x) (inc y) (- sf w)]
                      [(inc x) y sf]))))
        [0 0 0])
   (map pop)
   (take-while some?)))

=> (segment 10 2)
([0 0] [1 1] [2 1] [3 1] [4 1] [5 1 0] [6 2] [7 2] [8 2] [9 2] [10 2])

This is almost what we want, the only issue is that [0 0] is the only pixel on the first line:

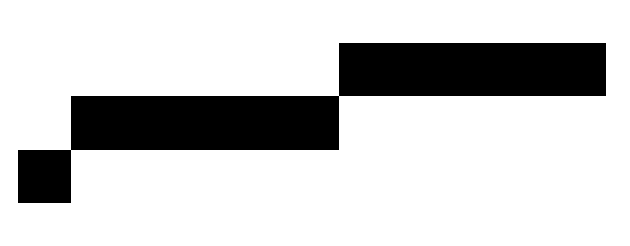
This is because we prevent sf from getting positive (that is to be below the line) so what we draw is the pixelated line "right above" the mathematical one.

To fix this we should shift our line down by half a pixel and we have seen that changing y by 1, changes sf by -w. To shift by half a pixel we only have to init sf with -w/2 instead of 0!

(defn segment
  "Returns a segment as a collection of integer coordinates from [0 0] to [w h]."
 [w h]
 {:pre [(pos? w) (<= 0 h w)]}
 (->> (iterate (fn [[x y sf]]
                (when (< x w)
                  (let [sf (+ sf h)]
                    (if (pos? sf)
                      [(inc x) (inc y) (- sf w)]
                      [(inc x) y sf]))))
        [0 0 (- (quot w 2))])
   (map pop)
   (take-while some?)))

=> (segment 10 2)
([0 0] [1 0] [2 0] [3 1] [4 1] [5 1] [6 1] [7 1] [8 2] [9 2] [10 2])

And this pixelated line is a lot nicer!

This algorithm is known as Bresenham's line algorithm

If you look closely at previous issue you may see that our circles suffered from a similar issue and their radius should be shifted by half a pixel too. This is left as an exercise to the reader 😉.

Closing thoughts

These algorithms are very sequential and incremental and have been shaped by hardware constraints of yore.

On modern hardware you can draw lines and circles using fragment shaders by being massively parallel (conceptually evaluating a pure function for each pixel) and by doing so many things become easier: antialiasing, line thickness and way more effects.

(Code for the above example)

I believe the same apply to programming in general, we are so entrenched culturally in sequential and hierarchical thinking that we can't leverage "relational" thinking in general.

What would a "Clojure" which emphasizes the use of sets instead of sequential collections look like?