04: Tracks
The fifth Procedural Note - describes the current logic for generating Tracks and next steps for getting a demo up.
This is the fifth Procedural Note.
The fourth promised, by 1/9, a playable demo of Rampant on the Tracks.
It's been a couple weeks since then. This Note does not include that demo - the first demo will be 2/6 at the latest.
This Note instead describes what took up the time in January slated for the demo, and the subsequent couple weeks - the procedural generation of the game's Tracks.
It leverages my Python library Voronout, as my previous demo did. It further modifies the generated diagram to create visually interesting Tracks that facilitate more challenging gameplay.
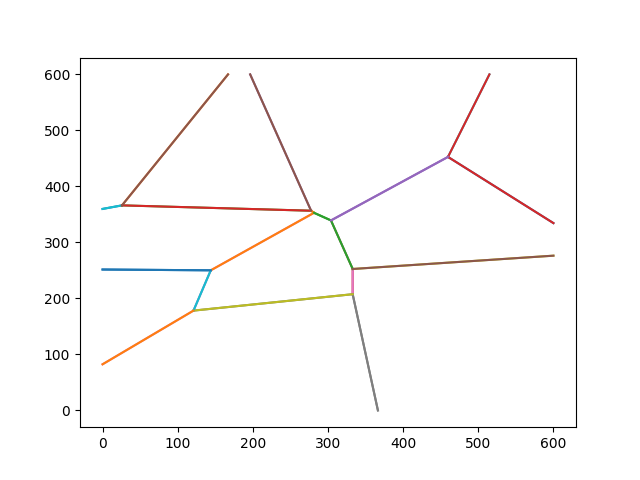
Compare an initially generated diagram
to that same diagram, modified:
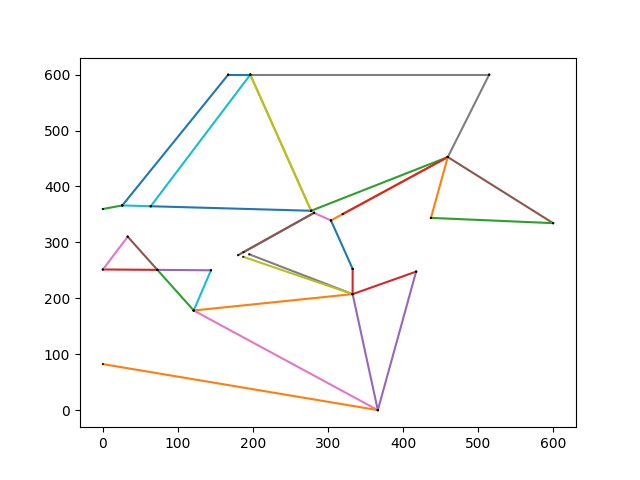
The first diagram is a natural-seeming arrangement of line segments. It is also one where every region created by the lines appears similar - three-to-five-sided-shapes of mostly similar length.
One such Track would look novel - but three, or five, or ten or more would start to look the same. The modification logic, applied to Voronout output, produces a greater variance in line segment lengths and the shapes created by them - and a longer-lasting sense of novelty.
How is this done?
Algorithmically - there are parameters initially provided by the user:
width: Track width
height: Track height
numRegions: number of sites on the Voronoi diagram
percentToProcess: percentage of the smallest edges in the diagram to reconnect
minPrimaryAnglesQuantile: value percentage to calculate the " minimum smallest angle " two line segments can make
minSecondaryAnglesQuantile: as above - this percentage is applied after the first one
minPrimaryEdgesLengthQuantile: value percentage to calculate the allowed " minimum length " of a line segment
minSecondaryEdgesLengthQuantile: as minSecondaryAnglesQuantile, but for minPrimaryEdgesLengthQuantile
The Track earlier was generated with
width: 600
height: 600
numRegions: 10
percentToProcess: 0.50
minPrimaryAnglesQuantile: 0.50
minSecondaryAnglesQuantile: 0.0833
minPrimaryEdgesLengthQuantile: 0.25
minSecondaryEdgesLengthQuantile: 0.05
width, height, and numRegions are used in generating the Voronoi diagram.
percentToProcess is used to determine which edges to reconnect:
edgesSorted = sorted(edgesToSort, key = lambda vde: vde.edge.edgeLength)
numEdgesToProcess = floor(len(edgesToSort) * percentToProcess)
Reconnection is the process of deleting an edge from the diagram and reconnecting its two vertices each to a different vertex (and not to themselves). We apply this to the smallest edges - a potential reconnection is near-guaranteed to be longer, creating a greater sense of variety.
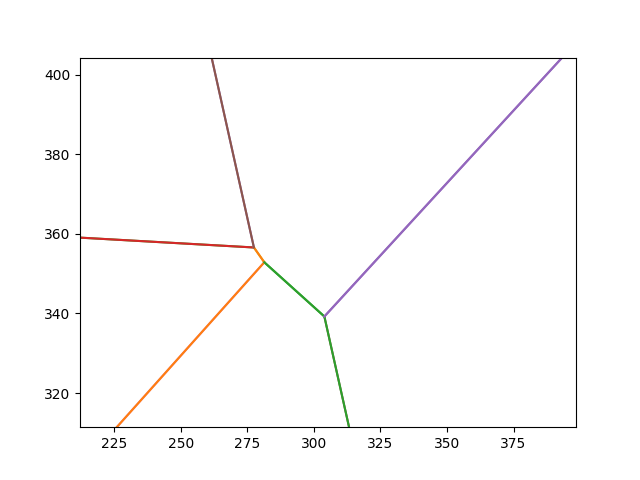
This can be illustrated by one reconnection done while constructing the example Track.
Here's the Track-in-progress before, zoomed in on for emphasis..
.. and here it is after:
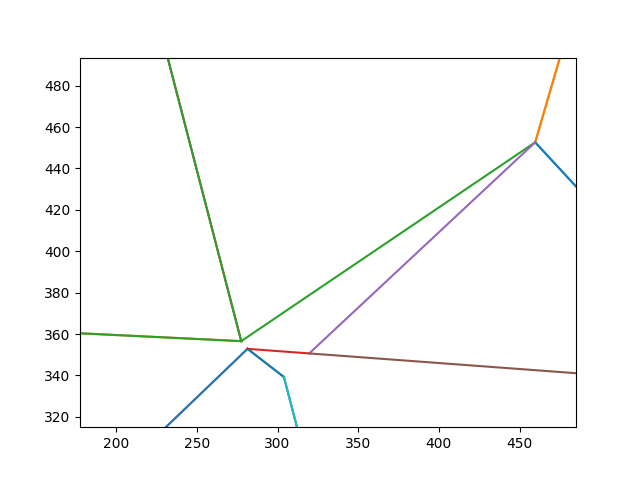
We've deleted the smallest of the visible edges here, reconnecting its two vertices - one diagonally upwards, one horizontally to the right. This not only creates visual variety, but also gameplay challenge - the path between the two vertices now takes multiple steps.
Reconnections are randomly chosen with equal probability from valid potentialConnections. We determine those by calculating, for each vertex edgePointId in the initial diagram, edgePointMinQuantile for each potentialConnectingVertex (other vertex it is not already connected to):
edgePoint = voronoiVertex(edgePointId)
for potentialConnectingVertex in potentialConnectingVertices:
potentialConnectingPoint = voronoiVertex(potentialConnectingVertex)
potentialConnectingDistance = scaledPointDistance(p1 = edgePoint, p2 = potentialConnectingPoint)
potentialConnection = VoronoiEdge(vertex0Id = edgePointId, vertex1Id = potentialConnectingVertex, neighborSiteId = None, edgeLength = potentialConnectingDistance)
potentialConnectionEdgeVertices = EdgeVertexInfo(vertex0Id = edgePointId, vertex1Id = potentialConnectingVertex, vertexDistance = potentialConnectingDistance)
edgePointMinQuantile = allEdgeAnglesMinQuantile(edge = potentialConnection, anglePointId = edgePointId)
if bool(edgePointMinQuantile):
potentialConnectionData[edgePointId].append(EdgePotentialConnectionInfo(connection = potentialConnectionEdgeVertices, connectionMinQuantileAngle = edgePointMinQuantile))
allEdgeAnglesMinQuantile():
def allEdgeAnglesMinQuantile(edge: VoronoiEdge, anglePointId: uuid4) -> float:
angleEdges = connectedByPoints[anglePointId]
edgeAngles = []
edgesProcessed = []
for angleEdge in angleEdges:
edgeAngle = angleBetweenEdges(edge1 = edge, edge2 = angleEdge.edge)
if edgeAngle > 0.0 and angleEdge.edge not in edgesProcessed:
edgeAngles.append(edgeAngle)
edgesProcessed.append(angleEdge.edge)
return numpy.quantile(edgeAngles, minQuantile) if edgeAngles else 0.0
The result in the case of our example, via numpy, is a value >= 50% all extant angles lines connected to anglePointId make.
We gather this value for each point..
connectionMinQuantiles = tuple((potentialConnectionDatum.connectionMinQuantileAngle for (_, potentialConnectionsInfo) in potentialConnectionData.items() for potentialConnectionDatum in potentialConnectionsInfo))
allConnectionsMinQuantile = numpy.quantile(connectionMinQuantiles, minPrimaryAnglesQuantile)
.. in order to calculate allConnectionsMinQuantile, the value >= 50% of all calculated quantiles.
This is used to generate potentialConnections:
potentialConnections = {}
for (pointId, potentialConnectionsInfo) in potentialConnectionData.items():
validPotentialConnections = list((validPotentialConnection.connection for validPotentialConnection in potentialConnectionsInfo if validPotentialConnection.connectionMinQuantileAngle >= allConnectionsMinQuantile))
potentialConnections[pointId] = validPotentialConnections
This helps to guard against the visual awkwardness of lines that look too close together. In the example Track, there is at most only one such - which further revision of the algorithm will eliminate.
Intersections are handled via minPrimaryEdgesLengthQuantile.
Intersections are a natural consequence of reconnection - a new connection made between vertices A and B could intersect edges C and D.
When that happens, we leverage minPrimaryEdgesLengthQuantile to filter out the " smallest " of the segments created by AB intersecting C or D.
intersectionEdgeLengths = tuple((intersectionEdgeInfo.edge.edgeLength for intersectionEdgeInfo in intersectionEdgeInfoToProcess))
intersectionEdgeLengthMinQuantile = numpy.quantile(intersectionEdgeLengths, minPrimaryEdgesLengthQuantile)
intersectionEdgesDataFiltered = tuple((intersectionEdgeInfo for intersectionEdgeInfo in intersectionEdgeInfoToProcess if intersectionEdgeInfo.edge.edgeLength >= intersectionEdgeLengthMinQuantile))
for intersectionEdgeInfo in intersectionEdgesDataFiltered:
intersectionEdge = intersectionEdgeInfo.edge
addEdgeToConnectedByPoints(vertexId = intersectionEdge.vertex0Id, edgeInfo = intersectionEdgeInfo)
addEdgeToConnectedByPoints(vertexId = intersectionEdge.vertex1Id, edgeInfo = intersectionEdgeInfo)
..
The effect of this can be seen in a snapshot of the Track-in-progress before..
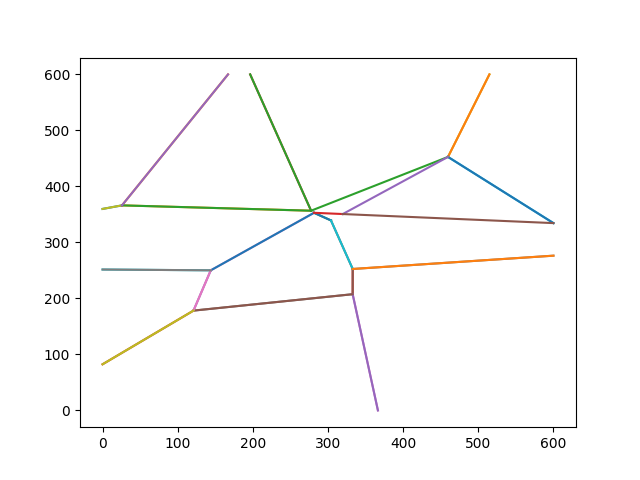
.. and after processing a reconnection that involves an intersection:
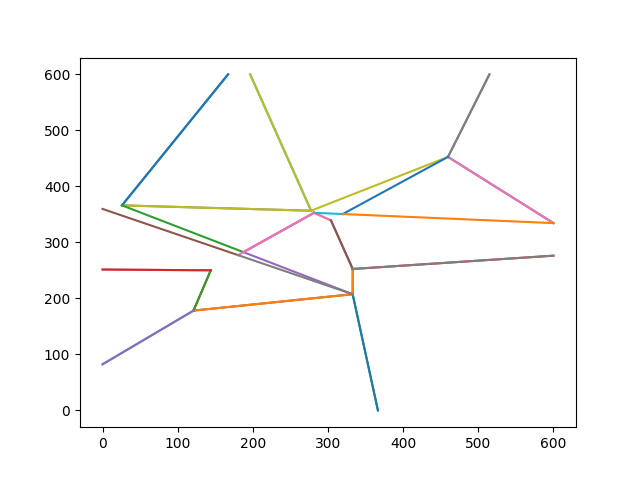
Part of an edge that was present " before " is no longer so " after " - as with reconnection, visual variety and gameplay challenge is created.
We continue reconnecting and handling intersections until we've finished initial edge processing.
The result is halfway there.
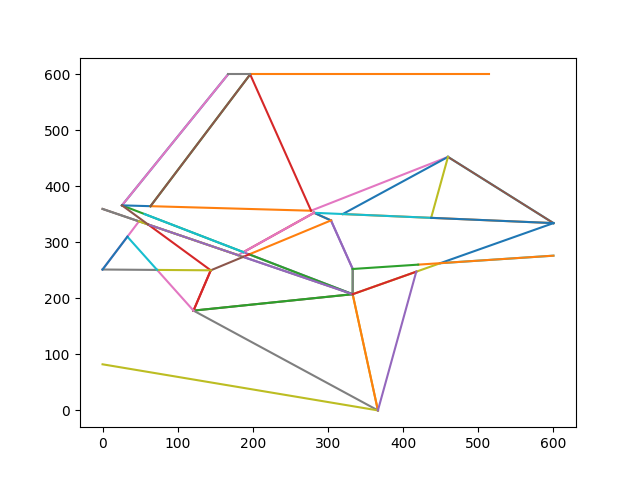
We just need to remove the too-small line segments and angles in this subset of segments.
This is where we use minSecondaryAnglesQuantile and minSecondaryEdgesLengthQuantile - and their smaller percentage values, appropriate for a smaller set of data.
We use the former to remove all edges that make an angle with their vertices' edges below allFilteredEdgesMinAngleQuantile (calculated in the same way as allConnectionsMinQuantile, against this smaller set).
for voronoiDiagramEdge in voronoiDiagramEdges:
vdEdge = voronoiDiagramEdge.edge
vdVertex0Id = vdEdge.vertex0Id
vdVertex1Id = vdEdge.vertex1Id
vertex0MinQuantile = allEdgeAnglesMinQuantile(edge = vdEdge, anglePointId = vdEdge.vertex0Id) >= allFilteredEdgesMinAngleQuantile
vertex1MinQuantile = allEdgeAnglesMinQuantile(edge = vdEdge, anglePointId = vdEdge.vertex1Id) >= allFilteredEdgesMinAngleQuantile
if vertex0MinQuantile and vertex1MinQuantile:
voronoiDiagramEdgesFiltered.append(voronoiDiagramEdge)
else:
filteredEdgesByVertex[vdVertex0Id] = filterEdgeOutOfEdgesInfo(edgesInfo = filteredEdgesByVertex[vdVertex0Id], edgeZeroVertex = vdVertex0Id, edgeOneVertex = vdVertex1Id)
filteredEdgesByVertex[vdVertex0Id] = filterEdgeOutOfEdgesInfo(edgesInfo = filteredEdgesByVertex[vdVertex1Id], edgeZeroVertex = vdVertex0Id, edgeOneVertex = vdVertex1Id)
We use the latter to remove all filteredVertexItem edges where doing so would not leave at least one vertex with only one relevant edge:
vertexesToDrawMinQuantile = numpy.quantile(vertexesToDrawEdgeLengths, 0.05)
vertexInfoToDrawByLength = []
belowMinQuantileEdges = []
for filteredVertexItem in filteredVertexInfoToDraw:
filteredVertexItem0 = filteredVertexItem.vertex0Id
filteredVertexItem1 = filteredVertexItem.vertex1Id
numFilteredEdgesAfterRemoval0 = len(filteredEdgesByVertex[filteredVertexItem0]) - 1
numFilteredEdgesAfterRemoval1 = len(filteredEdgesByVertex[filteredVertexItem1]) - 1
if filteredVertexItem.vertexDistance < vertexesToDrawMinQuantile and (numFilteredEdgesAfterRemoval0 > 1 and numFilteredEdgesAfterRemoval1 > 1):
if filteredVertexItem in filteredEdgesByVertex[filteredVertexItem0]:
filteredEdgesByVertex[filteredVertexItem0].remove(filteredVertexItem)
if filteredVertexItem in filteredEdgesByVertex[filteredVertexItem1]:
filteredEdgesByVertex[filteredVertexItem1].remove(filteredVertexItem)
belowMinQuantileEdges.append(filteredVertexItem)
else:
vertexInfoToDrawByLength.append(filteredVertexItem)
Once we've done that, we reconnect any edges left isolated in spite of the previous precaution..
for (filteredVertexId, filteredVertexEdges) in filteredEdgesByVertex.items():
if len(filteredVertexEdges) == 1:
for filteredVertexEdge in filteredVertexEdges:
otherFilteredVertexId = filteredVertexEdge.vertex0Id if filteredVertexId == filteredVertexEdge.vertex1Id else filteredVertexEdge.vertex1Id
if len(set(filteredEdgesByVertex[otherFilteredVertexId])) == 1:
if otherVertexId not in intersectionPoints:
filteredVertexChoices = tuple((EdgeVertexInfo(vertex0Id = filteredVertexChoice, vertex1Id = filteredVertexId, vertexDistance = scaledPointDistance(p1 = voronoiVertex(filteredVertexChoice), p2 = voronoiVertex(filteredVertexId))) for filteredVertexChoice in filteredVertices if filteredVertexChoice != filteredVertexId or filteredVertexChoice != otherFilteredVertexId or scaledPointDistance(p1 = voronoiVertex(filteredVertexChoice), p2 = voronoiVertex(filteredVertexId) > vertexesToDrawMinQuantile)))
filteredVerticesToPick = sorted(filteredVertexChoices, key = lambda fvc: fvc.vertexDistance)
filteredVertexPicked = filteredVerticesToPick[0]
vertexInfoToDrawByLength.append(filteredVertexPicked)
else:
filteredVertexChoices = tuple((EdgeVertexInfo(vertex0Id = filteredVertexChoice, vertex1Id = filteredVertexId, vertexDistance = scaledPointDistance(p1 = voronoiVertex(filteredVertexChoice), p2 = voronoiVertex(filteredVertexId))) for filteredVertexChoice in filteredVertices if filteredVertexChoice != filteredVertexId or filteredVertexChoice != otherFilteredVertexId or scaledPointDistance(p1 = voronoiVertex(filteredVertexChoice), p2 = voronoiVertex(filteredVertexId) > vertexesToDrawMinQuantile)))
filteredVerticesToPick = sorted(filteredVertexChoices, key = lambda fvc: fvc.vertexDistance)
filteredVertexPicked = filteredVerticesToPick[-1]
vertexInfoToDrawByLength.append(filteredVertexPicked)
if filteredVertexEdge in vertexInfoToDrawByLength:
vertexInfoToDrawByLength.remove(filteredVertexEdge)
(intersectionPoint reconnections are the edge closest to what they originally intersected with - other reconnections are to the edge farthest away from them.
In the first case, we're taking the opportunity of reconnection to re-create previously existing connections with at least slightly longer edge-lengths - in the second case, we're maximizing variety by going for the longest connection possible.)
.. and we're done!
What's next?
First, revision and optimization of this - despite the guards against " too close " angles and too small intersections, some still occur.
Next, demos illustrating this in a way beyond Matplotlib:
- one that shows off the visual look of Rampant on the Tracks, but not gameplay, on or before 2/6
- one that shows off gameplay, after the first (within a week of 2/6)
Both of those won't be hosted on GitHub, like previous demos, but on a new site.
Subscribe if you'd like to learn when those're available. Or if you're just curious.