Leetcode 797. How to Find All Paths From a Source to a Target in a Graph

Find all paths from the source to the target in a directed acyclic graph using Depth-First Search.

Problem statement

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

Example 1

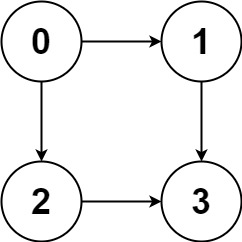
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: `0 -> 1 -> 3` and `0 -> 2 -> 3`.

Example 2

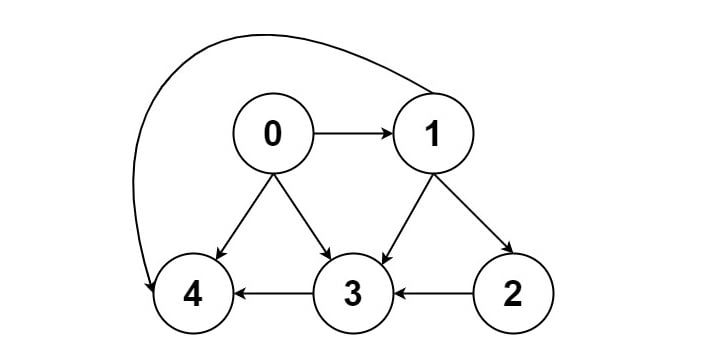
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

Example 3

Input: graph = [[1],[]]
Output: [[0,1]]

Example 4

Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]

Example 5

Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]]

Constraints

• n == graph.length.
• 2 <= n <= 15.
• 0 <= graph[i][j] < n.
• graph[i][j] != i (i.e., there will be no self-loops).
• All the elements of graph[i] are unique.
• The input graph is guaranteed to be a DAG.

Solution: Depth First Search (DFS)

This problem is exactly the Depth-first search algorithm.

Code

#include <vector>
#include <iostream>
using namespace std;
void DFS(vector<vector<int>>& graph, 
         vector<vector<int>>& paths, 
         vector<int>& path) {
    for (auto& node : graph[path.back()]) {
        path.push_back(node);
        if (node == graph.size() - 1) {
            paths.push_back(path);
            path.pop_back();
        } else {
            DFS(graph, paths, path);
        }
    }
    path.pop_back();
}
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
    vector<vector<int>> paths;
    vector<int> path = {0};
    DFS(graph, paths, path);
    return paths;
}
void printPaths(vector<vector<int>>& paths) {
    cout << "[";
    for (auto& p : paths) {
        cout << "[";
        for (auto& node : p) {
            cout << node << ",";
        }
        cout << "],";
    }
    cout << "]\n";
}
int main() {
    vector<vector<int>> graph = </span><span class="mi">1</span><span class="p">,</span><span class="mi">2</span><span class="p">},{</span><span class="mi">3</span><span class="p">},{</span><span class="mi">3</span><span class="p">},{;
    auto paths = allPathsSourceTarget(graph);
    printPaths(paths);
    graph = </span><span class="mi">4</span><span class="p">,</span><span class="mi">3</span><span class="p">,</span><span class="mi">1</span><span class="p">},{</span><span class="mi">3</span><span class="p">,</span><span class="mi">2</span><span class="p">,</span><span class="mi">4</span><span class="p">},{</span><span class="mi">3</span><span class="p">},{</span><span class="mi">4</span><span class="p">},{;
    paths = allPathsSourceTarget(graph);
    printPaths(paths); 
}

Output:
[[0,1,3,],[0,2,3,],]
[[0,4,],[0,3,4,],[0,1,3,4,],[0,1,2,3,4,],[0,1,4,],]

Code explanation

This code performs a Depth First Search (DFS) to find all possible paths from the source node (0) to the target node (graph.size() - 1) in a given directed graph represented as an adjacency list.

The DFS function explores the graph starting from the current node, and if it reaches the target node, it adds the path to the paths vector. Otherwise, it continues the DFS exploration from the neighboring nodes.

The allPathsSourceTarget function initializes the paths vector and a path vector that starts at the source node (0). It then calls the DFS function to traverse the graph, and once the traversal is complete, it returns the paths vector containing all possible paths from the source to the target node.

Complexity

The runtime complexity depends on a few factors:

• Number of nodes (N) and edges (E) in the graph.
• Number of paths between the two nodes.

In the worst case, DFS will explore all nodes in the graph. This happens when:

• The graph is dense (high E compared to N).
• There are many paths between the two nodes.

To find all paths between two nodes, DFS will have to explore the entire search space. So in the worst case, the complexity is O(N + E).

• Runtime: O(N + E), where N = graph.length and E is the number of the graph's edges.
• Extra space: O(N) (the vector path).

Thanks for reading!

I hope you enjoyed this content. Don't keep it to yourself! Share it with your network and help each other improve your coding skills and advance your career!

Nhut Nguyen, the author of The Problem Solver's Guide To Coding.