Leetcode 59. How To Go Around A Square Matrix In Spiral Order
Generate an `n x n` matrix filled in spiral order from 1 to n^2 in C++.
Problem statement
Given a positive integer n, generate an n x n matrix filled with elements from 1 to n^2 in spiral order.
Example 1
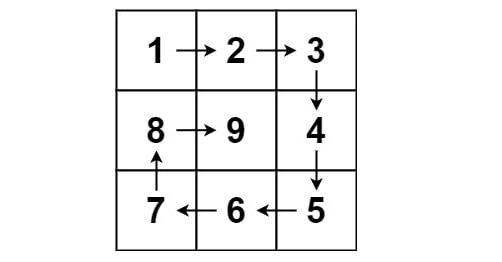
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]
Example 2
Input: n = 1
Output: [[1]]
Constraints
1 <= n <= 20.
Solution
- Starting from the top left of the matrix.
- Going along the spiral direction.
- Put the value to the matrix, starting from
1.
Code
#include <vector>
#include <iostream>
using namespace std;
enum Direction {RIGHT, DOWN, LEFT, UP};
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> m(n, vector<int>(n));
int bottom = n - 1;
int right = n - 1;
int top = 0;
int left = 0;
int row = 0;
int col = 0;
Direction d = RIGHT;
int a = 1;
while (top <= bottom && left <= right) {
m[row][col] = a++;
switch (d) {
case RIGHT: if (col == right) {
top++;
d = DOWN;
row++;
} else {
col++;
}
break;
case DOWN: if (row == bottom) {
right--;
d = LEFT;
col--;
} else {
row++;
}
break;
case LEFT: if (col == left) {
bottom--;
d = UP;
row--;
} else {
col--;
}
break;
case UP: if (row == top) {
left++;
d = RIGHT;
col++;
} else {
row--;
}
break;
}
}
return m;
}
void printResult(vector<vector<int>>& m) {
cout << "[";
for (auto& r : m) {
cout << "[";
for (int a : r) {
cout << a << ",";
}
cout << "]";
}
cout << "]\n";
}
int main() {
auto m = generateMatrix(3);
printResult(m);
m = generateMatrix(1);
printResult(m);
}
Output:
[[1,2,3,][8,9,4,][7,6,5,]]
[[1,]]
Code explanation
- The code creates a 2D vector
mof sizen x nto represent the square matrix. It initializes it with all zeros. - It defines variables
bottom,right,top, andleftto keep track of the boundaries of the matrix. Initially, they are set to the indexes of the outermost rows and columns of the matrix. - The code initializes
rowandcolto 0, representing the current position in the matrix. - It creates an enum
Directionto represent the current direction of movement (RIGHT,DOWN,LEFT,UP). It initializesdtoRIGHTto start moving to the right. - The code initializes an integer
ato 1, which will be used to fill the matrix with incrementing values. - It uses a while loop to traverse the matrix and fills it with values as long as the
topboundary is less than or equal to thebottomboundary and theleftboundary is less than or equal to therightboundary. - Inside the loop, it fills the current position
(row, col)in the matrix with the valueaand incrementaby 1. -
The code uses a
switchstatement based on the current directiondto determine the next move:- If
dis RIGHT, it checks ifcolhas reached therightboundary. If it has, it moves to the next direction (DOWN) and updaterowaccordingly; otherwise, incrementcol. - Similar logic is applied for the
DOWN,LEFT, andUPdirections, adjustingrowandcolaccordingly and changing direction when needed. 9. Once the loop is complete, the matrix is filled in a spiral order, and the function returns the filled matrix.
- If
Complexity
- Runtime:
O(n^2), wheren x nis the size of the matrix. - Extra space:
O(1).
Don't miss what's next. Subscribe to LeetSolve - Level Up Your Coding Skills:
Share this email: