Leetcode 235. How To Find a Nearest Common Ancestor In a Binary Search Tree

This email edition discusses finding the Lowest Common Ancestor in a Binary Search Tree using recursion.

Problem statement

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: "The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself)."

Example 1

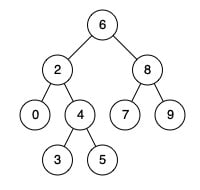
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3

Input: root = [2,1], p = 2, q = 1
Output: 2

Constraints

• The number of nodes in the tree is in the range [2, 10^5].
• -10^9 <= Node.val <= 10^9.
• All Node.val are unique.
• p != q.
• p and q will exist in the BST.

Solution: Recursion

Note that in a BST, the values of a node and its children left and right satisfy

left.value < node.value < right.value.

It lets you know which branch (left or right) of the root the nodes p and q belong to.

Code

#include <iostream>

using namespace std;
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if (p->val < root->val && q->val < root->val) {
        return lowestCommonAncestor(root->left, p, q);
    } else if (root->val < p->val && root->val < q->val) {
        return lowestCommonAncestor(root->right, p, q);
    }
    return root;
}
int main() {
    TreeNode zero(0);
    TreeNode three(3);
    TreeNode five(5);
    TreeNode four(4);
    four.left = &three;
    four.right = &five;
    TreeNode two(2);
    two.left = &zero;
    two.right = &four;
    TreeNode seven(7);
    TreeNode nine(9);
    TreeNode eight(8);
    eight.left = &seven;
    eight.right = &nine;
    TreeNode six(6);
    six.left = &two;
    six.right = &eight;

    cout << lowestCommonAncestor(&six, &two, &eight)->val << endl;
    cout << lowestCommonAncestor(&six, &two, &four)->val << endl;
    cout << lowestCommonAncestor(&two, &two, &zero)->val << endl;
}

Output:
6
2
2

Code explanation

1. The function takes three arguments: root, p, and q. root represents the root node of the BST, while p and q represent the two nodes for which we want to find the lowest common ancestor.
2. The code starts with a recursive approach and a divide-and-conquer strategy. It checks whether the values of p and q are less than the value of the current root node or greater than the value of the current root node. These comparisons are made using the values stored in p->val, q->val, and root->val.
3. If both p and q are less than root->val, it means that both nodes p and q are in the left subtree of the current root. In this case, the code recursively calls lowestCommonAncestor(root->left, p, q) to search for the LCA in the left subtree.
4. If both p and q are greater than root->val, it means that both nodes p and q are in the right subtree of the current root. In this case, the code recursively calls lowestCommonAncestor(root->right, p, q) to search for the LCA in the right subtree.
5. If neither of the above conditions is met, it means that one node is in the left subtree, and the other is in the right subtree, or one of them is the current root node itself. In either case, the current root node is the lowest common ancestor, and the code returns root.
6. The recursion continues until it finds the LCA or reaches a null node (indicating that one of the nodes p or q was not found in the subtree). In the latter case, the code returns root, which might be a valid LCA if one of the nodes is present in the subtree or nullptr if both nodes are not in the tree.

Complexity

This solution leverages the properties of a BST, where the left subtree contains nodes with values less than the root, and the right subtree contains nodes with values greater than the root, to efficiently find the lowest common ancestor of two nodes p and q.

• Runtime: O(h), where h is the height of the tree. In a balanced BST, this height is typically log(N) for N nodes.
• Extra space: O(1).

Thanks for reading!

I hope you enjoyed this content. Don't keep it to yourself! Share it with your network and help each other improve your coding skills and advance your career!

Nhut Nguyen, the author of The Problem Solver's Guide To Coding.