Maclaurin Expansion

Working out the correct algorithm we need will require a clear idea of what an exact solution may look like.

Reconsider what I just wrote: taken glibly, I'm saying an approximate solution requires an exact answer. That's not as much a contradictory statement it seems, but a mathematical point of view. A scientist might say, contra-wise, that the approximation requires data acquired via observation. That's the way scientists since Copernicus and Galileo developed models of the universe. That's how the proliferation of AI machines today have been built. We need something "real" to compare with our approximation.

In 1742, Colin Maclaurin published a textbook on Isaac Newton's discoveries in calculus. This book contains a crucial generalization of a theorem by Taylor, whose series precisely reproduces differentiable functions. If you can differentiate a function n times, then you can also write down n+1 terms of a Maclaurin-Taylor series. This series, which may be infinite in length, will match the output of the original function. In the controversial treatment of calculus at the time, the ultimate term may be said to "vanish." This mathematical imprecision can be remedied with a more formal approach, but in the context of this project, we can use the "vanishing" quality of the asymptotic series to serve as intuition for our approximation strategy.

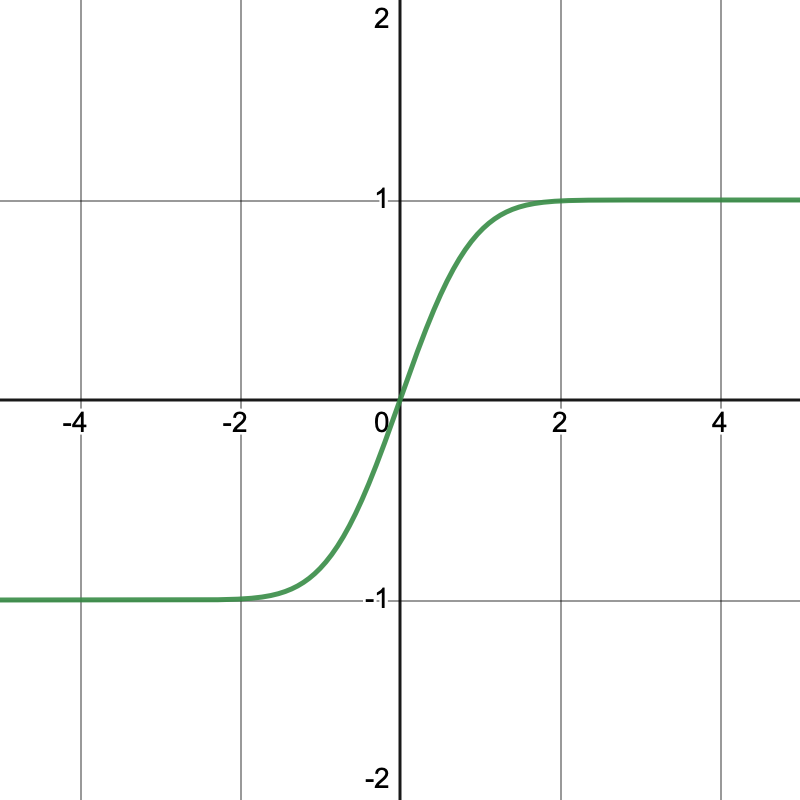
The first image shows the "true" graph of erf as sketched in Desmos. In fact, this too is an approximation, likely using the same function we're reconstructing in this project. Being a "best" approximation, it's good enough to show us what the "true" graph looks like.

Recall the integral definition of erf is written

The Maclaurin series expansion of this integral is

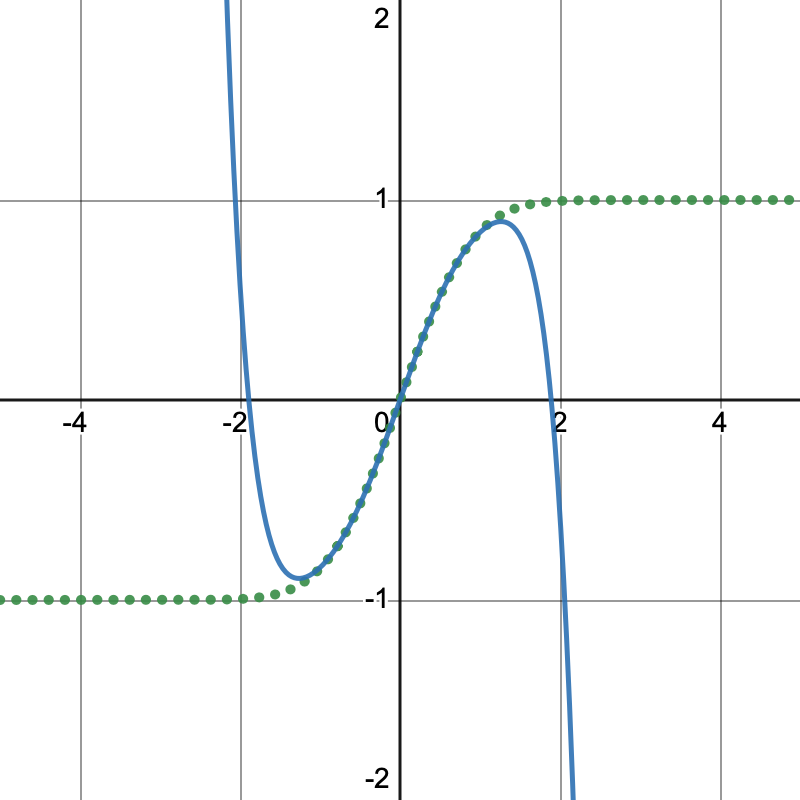
I've written out just four terms of the series; these are the same four terms documented in the Sun Microsystems comment. By taking just these four terms, we have an asymptotic representation that's precise -- up to a point. The second image displays a sketch of the Maclaurin series. Notice how it drops off after x = 1 whereas we expect the real function to approach erf(∞) = 1.

This tells us that four terms of the Maclaurin series only looks good enough an approximation between negative and positive one. We could produce more terms, but then we need to do more computational work. It'd be nice to use a simpler approximation - and that's what our project's about.