I struggled to understand this lemma, which I first encountered in Powell, Chapter 4.1 This was a problem, as the lemma provides the key to constructing the required matrix to identify eigenvalues for the rational approximation I’m seeking. But don’t worry about that technical jargon for now, let’s focus on making sense of the lemma defining Lagrange polynomials.
TLDR: This lemma provides a formal definition for interpolation on available data by proving that a polynomial of the desired degree exists. It’s used to prove that such a polynomial is unique, a fact that enables us to systematically search for useful approximating functions. The lemma will be used in a future post to create an algorithm for rational approximations by canceling out non-linear terms.
A better discussion of the Lagrange polynomial and its motivation is found in Süli and Mayers2:
If the function values f(x) are known for all x in a closed interval of the real line, then the aim of polynomial interpolation is to approximate the function f by a polynomial over this interval. Given that any polynomial can be completely specified by its (finitely many) coefficients, storing the interpolation polynomial for f in a computer will be, generally, more economical than storing f itself.
That’s our motivation. Well, not quite. That’s our justification for doing this project. My motivation, at least, is to make sense of why these techniques work at all, reproducing standard results through the effort.
We start with known independent data x_i and known dependent data y_i for i = 0, …, n. We presume this data may be reproduced from some smooth function f(x) = y. I say “presume” here because f may be defined explicitly, like erf, or we might simply have good reason to suspect that, given any input x the output y will correspond with the previously known data points (x_i, y_i). Importantly, we want this to be smooth, that is, continuously integratable.
We could guess at functions that produce the same data. But we already have sample data; we can simply “draw a smooth line” through the dataset. The polynomial describing this line will be our approximation.
Let n > 0 be the degree of the approximating polynomial. We gather the data x_i and y_i for i = 0, …, n, and we fix some k between 0 and n. Define the product
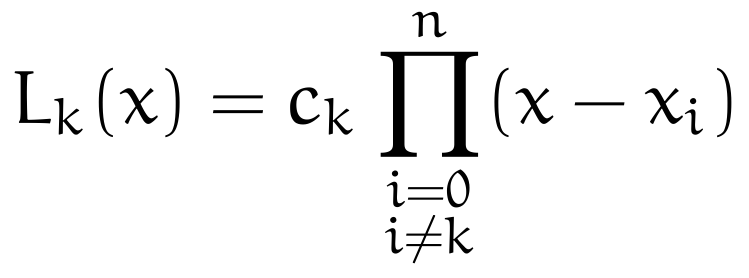
where c_k is a constant.
To ensure that this function passes through the data points we’ve meticulously collected, we place a constraint on its output values
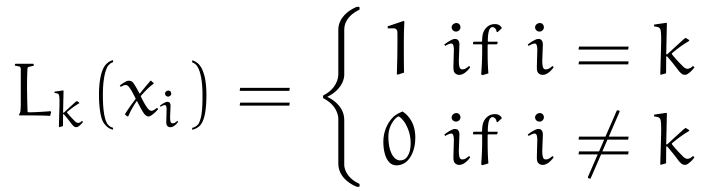
Note the subscript here, as it’s important. We have for each L_k, if the input comes from the kth sample, we “pick” that sample; otherwise, we do not.3
Let’s use this constrain immediately to observe that the kth input will give one, and use it to derive a kth constant, as such
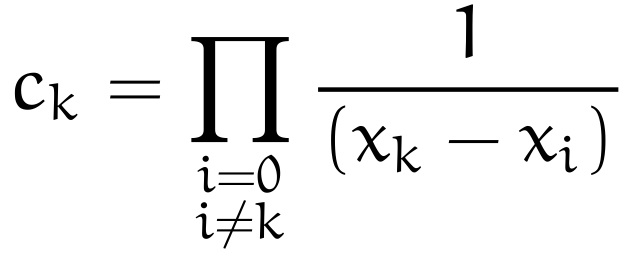
which we can then immediately reinsert into the original definition of L_k to get the polynomial
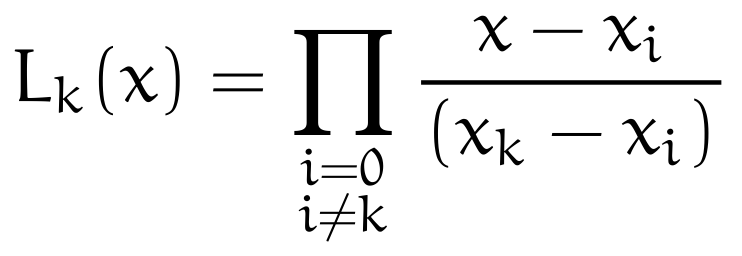
Recap: this function takes any x on a closed interval as input and outputs a real number. There’s three potential outputs:
1if the input is in our data set and its index matchesk0if the input is in our data set and its index does not matchksome real number between
0and1determined by our data set
The outputs from this function clearly reside in the closed interval [0, 1]. The function also gives a polynomial with degree n. The final thing we have to understand here is that, because we have known values y_i for each x_i, we can create a polynomial from L_k by linear combination. Hence
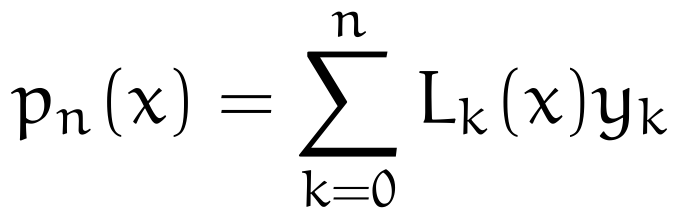
What does this do? Keep in mind our three possibilities for L_k. If the input x happens to be in our data set, only the L_k matching its index will equal 1, all others will equal 0. In other words, L_k “picks out” the matching y_k, making the identity
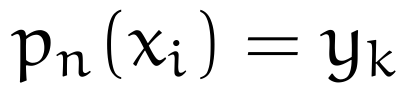
hold as required. For any x not in our data set, the function L_k scales the combinations of known outputs to the nearest neighboring value.
The technical term for “scaling a combination of known outputs to the nearest neighboring value” is interpolation.
Looking Ahead
This argument is presented as a lemma in Süli and Mayers as a prelude to their Theorem 6.1, the Lagrange Interpolation Theorem, which asserts that unique approximation polynomials exist given the data. The same argument, with different presentation, is given as part of the proof of Powell’s Theorem 4.1, which is the same uniqueness assertion. No doubt Süli and Mayers used Powell as their primary source. They did something very helpful, however, in their book by extracting this argument as a separate lemma. This is something Powell should have done, in my opinion, since he directly invokes the (implied) lemma in Section 10.2, where non-linear terms in a system of rational approximation equations make finding coefficients essentially impossible without canceling out terms via the lemma.
I’ll write about my mistake and how to over come it next time. Thanks for reading through — this topic is not easy!
Powell, MJD. Approximation Theory and Methods. Cambridge University Press (1981) Buy Borrow
Süli, E and Mayers, D.F. An Introduction to Numerical Analysis. Cambridge University Press (2003) Buy Borrow
In a certain sense, if the input is not in our data, we find some data in between that’s calculated via a product ratio of all samples.