Error Function
Say you expect a normal or Gaussian distribution for some data. How do you calculate the probability that a variate or instance of the data falls within an expected range? Note that, analytically, the distribution does admit all values from negative to positive infinity, just not with the same probability ratio.
Recall that the normal or Gaussian distribution is written as
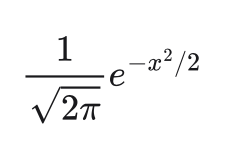
with the parameters for mean and standard deviation assumed to be zero and one, respectively. To acquire the desired probability, we integrate to express
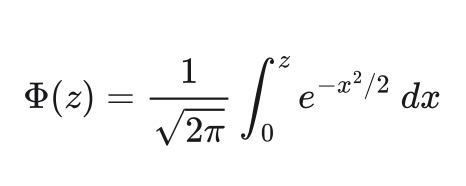
This integral is known as the "error function", or erf in ISEE Standard 1003.1-2017 and the ISO C standard library. The function effectively tells us the probability of a variate z or less.
This phrase, or less, should hint at a potential issue. For one, it's a bound on the theoretical probability, not an observed frequency in the data. Second, the representation of this probability may have errors of its own, given the finite abilities of floating point arithmetic.
A specific problem occurs when the theoretical probability gets close to 1. Subtracting the computed result from 1 creates a round-off error. So we need to specify a complimentary integral
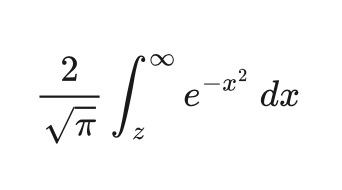
which is implemented separately as erfc to avoid the round-off when suspecting a close computation.
Before Dennis Ritchie developed the C language at Bell Labs in the 1970s, Abramowitz and Stegun printed coefficients for various approximations to be used in erf and erfc by computer engineers and applied mathematicians. I first became interested in this function when I saw a mysterious set of floating point constants in the Go source code -- how in the world did the authors of this code determine these floating point values?
Reading Abramowitz and Stegun, definitions 7.1.1 and 7.1.2 for erf and erfc respectively provide a handful of approximation methods, which directly compute coefficients on a selected range of the integrals. These authors take their methods from Hasting's "Approximations for Digital Computers"; the Go implementation itself derives from a Sun Microsystems implementation for FreeBSD from the early 1990s. Despite being much later in construction, the Go implementation basically simplifies the C code written by Sun, and the constants themselves have been chosen for specific ranges of the integrals with the variate from 0 to 28.
All these coefficients have been discovered via an approximation methodology similar, if not identical, to those used by Abramowitz and Stegun and by Hastings. I imagine, but have not confirmed, that the choice of 28 for the upper bound on the approximations has to do with the bits available in certain floating point representations. Since this all derives from the Gaussian distribution, values outside the select range can be normalized (no pun!) to fit the computational range of the functions.
References
- https://mathworld.wolfram.com/NormalDistribution.html
- https://mathworld.wolfram.com/Erfc.html
- https://www.mathworks.com/help/matlab/ref/erfc.html
- https://www.commandlinux.com/man-page/man3/erfc.3.html
- https://pubs.opengroup.org/onlinepubs/9699919799/
- https://pubs.opengroup.org/onlinepubs/9699919799/functions/erf.html#
- https://www.commandlinux.com/man-page/man3/erf.3.html
- https://cs.opensource.google/go/go/+/refs/tags/go1.22.0:src/math/erf.go;l=189
- https://personal.math.ubc.ca/~cbm/aands/abramowitz_and_stegun.pdf