Complimentary Error Function

I wrote previously about the error function erf, and how round-off error necessitates the complementary error function, defined as erfc = 1 - erf. In this essay, I want to derive the integral involved.

Begin with the identity

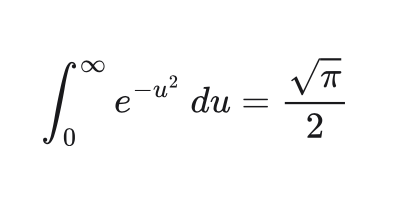
We'll justify this identity conceptually later. Our goal for now is to work backwards to find the integral expression for erfc. This will proceed in three steps; you'll need to watch closely if you're unaccustomed to calculus. First, we'll rearrange the identity to equal one; second, we'll split the integral into two integrals at an arbitrary point z, then we'll rearrange to show our result.

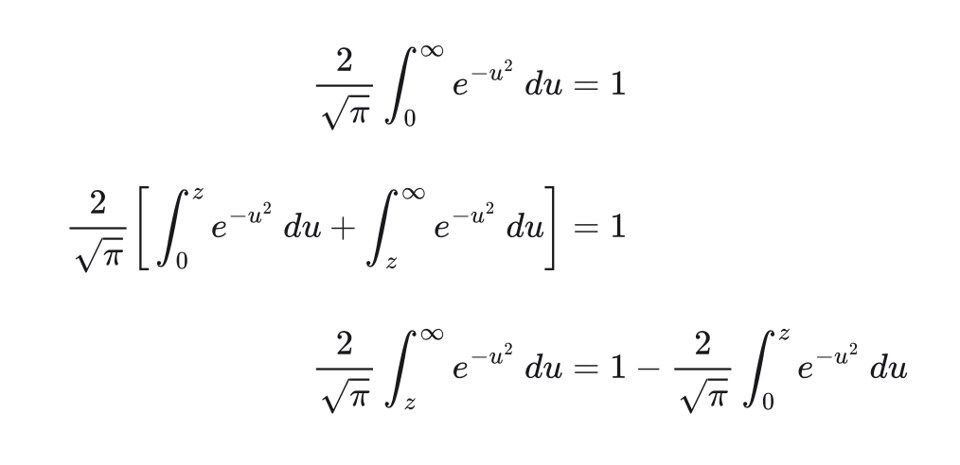
Recognize the integral on the right as the same as erf shown earlier, making the integral on the left our definition for erfc. But this seems too easy! Why should these functions behave like this, and why should we care?

Let's work our intuition a bit more, by trivially taking a limit on both sides

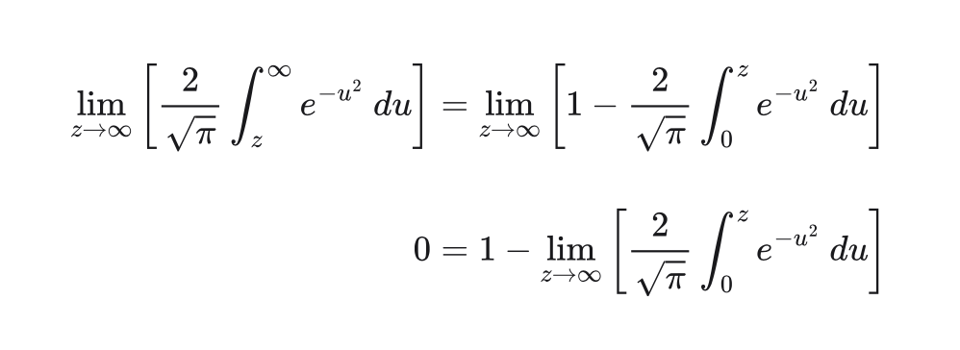
Again, this expression is trivial. Using the identity we started with, the limit in the last line resolves to

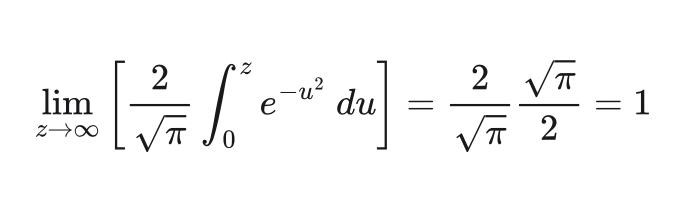
But! This expression says something very specific that holds true in mathematics but fails in practical computing. The expression says

if we input larger and larger values for z into erf, we should get an output closer and closer to 1.

Likewise, if we pause on our evaluation of the left hand limit, we see the complementary idea that

if we input larger and larger values for z into erfc, we should get an output closer and closer to 0.

Yet we simply cannot do either of these two things mechanically. The machine has finite representation in its floating point implementation. On 64-bit machines, Go programs can represent a float no larger than about 1.8 * 10^308 and no smaller than 3.9 * -10^324. These are admittedly absurdly large (small) numbers... yet from a mathematical point of view, they're exceedingly far from infinity and from zero. Back when machines were not so plentiful and inexpensive as they are now, the finite limitations were much more troublesome.

Knowing that the complimentary side uses z as a lower bound means we can make it very large -- as close to our largest floating point representation as we can get. In practice, infinity becomes a simple check that z < math.MaxFloat64, cutting off the computation to avoid rounding errors. For very large z or very small z, the programmer can switch her usage of erf or erfc to safely compute an error, without rounding prematurely.

An integral due to Laplace

Now the really important question: what justifies the identity?

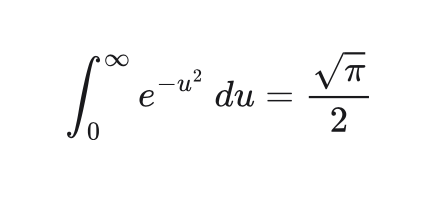
My intuition tells me that, if we work with the Gaussian in two dimensions, we should find that a correlation of two variates is at an extreme when the central angle is orthogonal, i.e., when

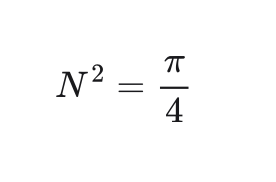
This intuition may be faulty, but it eventually helped me to re-create Simone Laplace's integral.

Start with the expression

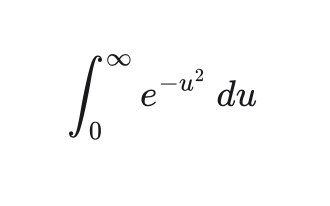
and make the substitutions

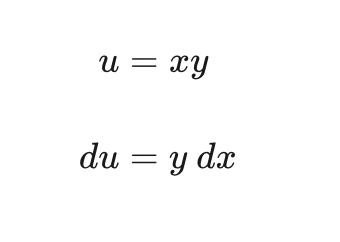
to get

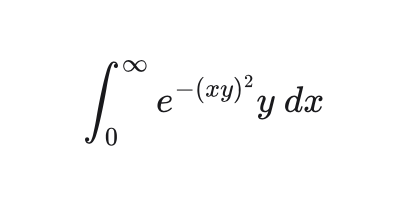
Since y is "free", we can replace it again with u and write the double integral

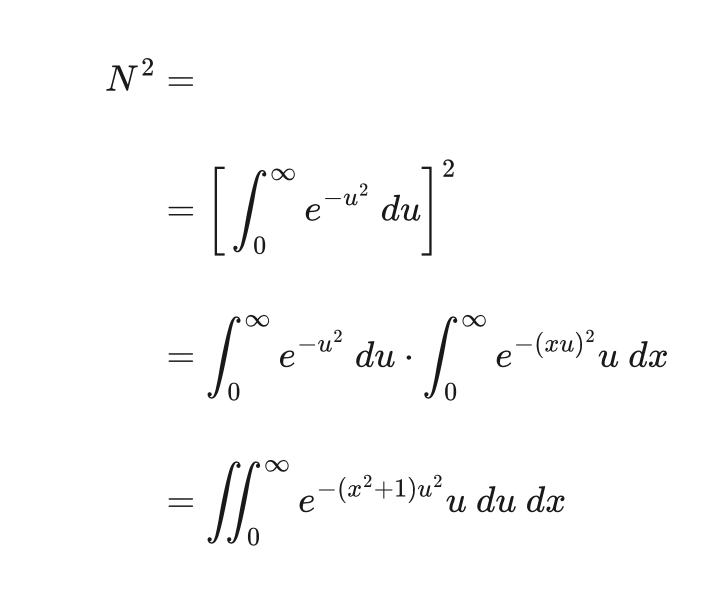
Now make another substitution for

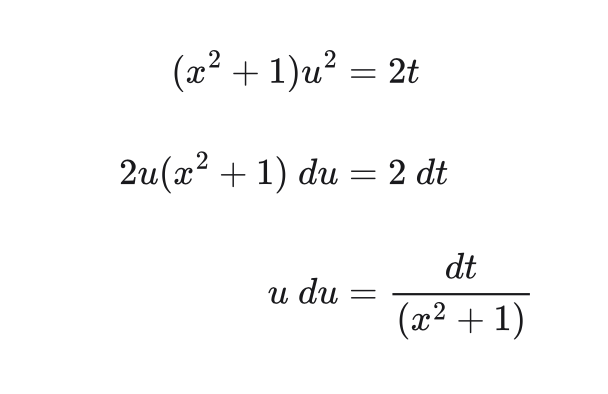
Now we have

Which matches what we wanted. Splitting the double integral is made possible by Fubini's Theorem, and the evaluation of the arc-tangent can be found in a table of integrals (which I plan to publish separately).

Fun stuff! The basic functionality behind our lower level computing resources relies upon the same mathematical concept from two hundred years ago

References

• http://www.rskey.org/CMS/the-library/?view=article&id=11
• https://maa.org/programs/maa-awards/writing-awards/the-evolution-of-the-normal-distribution
• https://sites.math.washington.edu/~morrow/335_12/fubini.pdf
• https://www.cambridge.org/9780521796361
• https://www.york.ac.uk/depts/maths/histstat/normal_history.pdf