This project's guided by the concept that we write mathematics. Thoughts and discussion occur, but mathematics doesn't happen, in my sense, until its been written down.
essay originally published at mathbook.cafe
The way we do mathematics changes across generations. The tools we use to write down thoughts and discussion, thereby doing mathematics, changes as the people who do the writing change. Most recently, the Lean 4 programming language has become an active environment for doing mathematics. Lean allows mathematicians to write down, in compilable code, formal representations of mathematical statements. Before automated theorem provers like Lean, professional mathematicians wrote down, also in code, typesetting directives to display formally presentable mathematical writing. New languages, like Typst, continue to be invented for this task.
Yet in order to have formalities to compile or symbols to typeset, mathematicians must have already specified a language and symbology. Where, for instance, did the Greek letter $\pi$, come to represent the ratio of a circle's circumference to its diameter?
Georges Ifrah's book, The Universal History of Computing, gives an exhaustive summary of the origins of present day mathematical symbology.
- 3rd Century BCE: Brahmin writers (Maurya, present day India) begin using the precursors for the decimal numerals
- 1440: Laurens Janszoon (Holland) experiments with typographic printing
- 1489: Johann Widmann (Germany) uses + and - for addition and subtraction, respectively
- 16th Century CE: Europeans generally adopt the Indian modernized decimal numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- 1525: Christoph Rudolff (Germany) uses √ for the square root
- 1540: Johannes Gutenberg (Germany) develops metallic type, reinventing printing for Europeans
- 1557: Robert Recorde (England) uses = for equality
- 1582: Simon Stevin (Flanders) uses 679 (0) 5 (1) 6 (2) for decimal numerals, where the parentheses denote the "order" of the decimal terms
- 1591: François Viéte (France) uses vowels A, E, ... for unknown variables and constants B, C, ... for undetermined constants.
- 1592: Giovanni Magini (Italy) uses 679.56 for decimal numerals, modernizing Stevin's notation
- 1608: Willebord Snellius (Holland) uses 679,56 for decimal numerals, still used in Europe
- 1631: William Oughtred (England) uses × for multiplication
- 1637: René Descartes uses a, b, c, ... for constants and ..., x, y, z for unknowns, modernizing Viéte's notation, and introduces a^2, etc, for exponential powers
- 1656: John Wallis expands exponential notation to include fractional and negative powers; he also uses ∞ for infinity
- 1670: Gottfried Wilhelm Leibniz (Germany) uses dx/dt for differential ratios and ∫ for integrated or summed differentials
- 1670: Isaac Newton (England) uses ẋ for rate of change
- 1683: Jacob Bernoulli (Switzerland) uses e for the limit of compound interest
- 1706: William Jones (England) uses π for the ratio of circumference to diameter
- 1736: Leonhard Euler (Switzerland) popularizes π
- 1794: Euler uses i for the negative square root
Most of what I write about has its typographic origin in the timeline above; by the end of the 19th century, calculus will have achieved its modern form and formulation. I'm fascinated, in reviewing this history, and all the tremendous detail Ifrah provides in his book, by how much the technology of the printing press directly influenced the expression of mathematics during the European Renaissance and Enlightenment.
Amazingly, the "modern" ideas of the limit concept aren't expressible without the pre-modern invention of the moveable type. (My project exists precisely because I'm able to use the concise modern notation as a foothold for more discursive expressions.) Even more amazing, once the Gutenberg press launched Europeans from their provincial, second-hand intellectual past, some of the smartest people who ever lived - Descartes, Wallis, Leibniz, Newton - suddenly had the tools to send their ideas worldwide.
Ifrah's translator, Robert Laffont, includes this lovely "tailpiece" to his chronological summary
> We have now met the five fundamental numbers of mathematics: 0 (the zero of the number-system); 1 (the unit); e = 2.7182818... (the base of natural logarithms); π = 3.1415926... (the ratio of the circumference of a circle to its diameter); and finally the "imaginary" number, the square root of -1, denoted by i = √-1. Between these five numbers there holds a startling relationship:
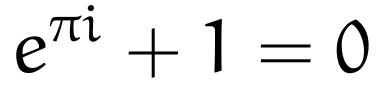
This relationship was discovered by Euler, but before he adopted the symbol $i$ sometime around the 1790s. Thus Euler would have originally written
