Solving LinkedIn Queens with SMT
For sure easier than solving it in SAT!
No newsletter next week
I’ll be speaking at Systems Distributed. My talk isn't close to done yet, which is why this newsletter is both late and short.
Solving LinkedIn Queens in SMT
The article Modern SAT solvers: fast, neat and underused claims that SAT solvers1 are "criminally underused by the industry". A while back on the newsletter I asked "why": how come they're so powerful and yet nobody uses them? Many experts responded saying the reason is that encoding SAT kinda sucked and they rather prefer using tools that compile to SAT.
I was reminded of this when I read Ryan Berger's post on solving “LinkedIn Queens” as a SAT problem.
A quick overview of Queens. You’re presented with an NxN grid divided into N regions, and have to place N queens so that there is exactly one queen in each row, column, and region. While queens can be on the same diagonal, they cannot be adjacently diagonal.
(Important note: Linkedin “Queens” is a variation on the puzzle game Star Battle, which is the same except the number of stars you place in each row/column/region varies per puzzle, and is usually two. This is also why 'queens' don’t capture like chess queens.)
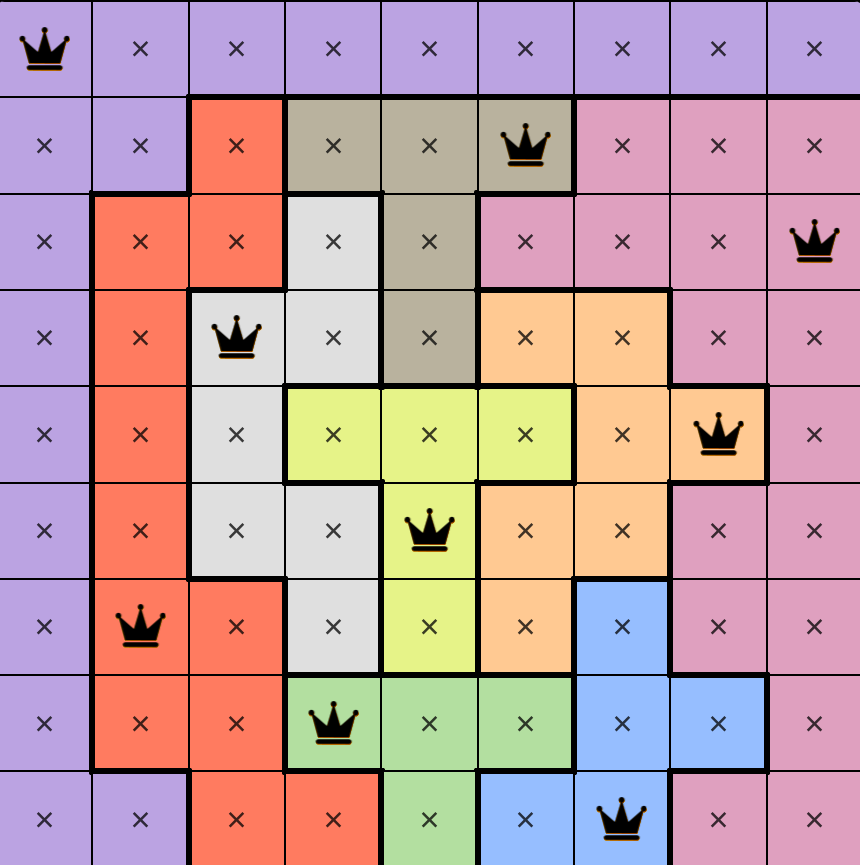
Ryan solved this by writing Queens as a SAT problem, expressing properties like "there is exactly one queen in row 3" as a large number of boolean clauses. Go read his post, it's pretty cool. What leapt out to me was that he used CVC5, an SMT solver.2 SMT solvers are "higher-level" than SAT, capable of handling more data types than just boolean variables. It's a lot easier to solve the problem at the SMT level than at the SAT level. To show this, I whipped up a short demo of solving the same problem in Z3 (via the Python API).
Full code here, which you can compare to Ryan's SAT solution here. I didn't do a whole lot of cleanup on it (again, time crunch!), but short explanation below.
The code
from z3 import * # type: ignore
from itertools import combinations, chain, product
solver = Solver()
size = 9 # N
Initial setup and modules. size is the number of rows/columns/regions in the board, which I'll call N below.
# queens[n] = col of queen on row n
# by construction, not on same row
queens = IntVector('q', size)
SAT represents the queen positions via N² booleans: q_00 means that a Queen is on row 0 and column 0, !q_05 means a queen isn't on row 0 col 5, etc. In SMT we can instead encode it as N integers: q_0 = 5 means that the queen on row 0 is positioned at column 5. This immediately enforces one class of constraints for us: we don't need any constraints saying "exactly one queen per row", because that's embedded in the definition of queens!
(Incidentally, using 0-based indexing for the board was a mistake on my part, it makes correctly encoding the regions later really painful.)
To actually make the variables [q_0, q_1, …], we use the Z3 affordance IntVector(str, n) for making n variables at once.
solver.add([And(0 <= i, i < size) for i in queens])
# not on same column
solver.add(Distinct(queens))
First we constrain all the integers to [0, N), then use the incredibly handy Distinct constraint to force all the integers to have different values. This guarantees at most one queen per column, which by the pigeonhole principle means there is exactly one queen per column.
# not diagonally adjacent
for i in range(size-1):
q1, q2 = queens[i], queens[i+1]
solver.add(Abs(q1 - q2) != 1)
One of the rules is that queens can't be adjacent. We already know that they can't be horizontally or vertically adjacent via other constraints, which leaves the diagonals. We only need to add constraints that, for each queen, there is no queen in the lower-left or lower-right corner, aka q_3 != q_2 ± 1. We don't need to check the top corners because if q_1 is in the upper-left corner of q_2, then q_2 is in the lower-right corner of q_1!
That covers everything except the "one queen per region" constraint. But the regions are the tricky part, which we should expect because we vary the difficulty of queens games by varying the regions.
regions = {
"purple": [(0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8),
(1, 0), (2, 0), (3, 0), (4, 0), (5, 0), (6, 0), (7, 0), (8, 0),
(1, 1), (8, 1)],
"red": [(1, 2), (2, 2), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (6, 2), (7, 1), (7, 2), (8, 2), (8, 3),],
# you get the picture
}
# Some checking code left out, see below
The region has to be manually coded in, which is a huge pain.
(In the link, some validation code follows. Since it breaks up explaining the model I put it in the next section.)
for r in regions.values():
solver.add(Or(
*[queens[row] == col for (row, col) in r]
))
Finally we have the region constraint. The easiest way I found to say "there is exactly one queen in each region" is to say "there is a queen in region 1 and a queen in region 2 and a queen in region 3" etc." Then to say "there is a queen in region purple" I wrote "q_0 = 0 OR q_0 = 1 OR … OR q_1 = 0 etc."
Why iterate over every position in the region instead of doing something like (0, q[0]) in r? I tried that but it's not an expression that Z3 supports.
if solver.check() == sat:
m = solver.model()
print([(l, m[l]) for l in queens])
Finally, we solve and print the positions. Running this gives me:
[(q__0, 0), (q__1, 5), (q__2, 8),
(q__3, 2), (q__4, 7), (q__5, 4),
(q__6, 1), (q__7, 3), (q__8, 6)]
Which is the correct solution to the queens puzzle. I didn't benchmark the solution times, but I imagine it's considerably slower than a raw SAT solver. Glucose is really, really fast.
But even so, solving the problem with SMT was a lot easier than solving it with SAT. That satisfies me as an explanation for why people prefer it to SAT.
Sanity checks
One bit I glossed over earlier was the sanity checking code. I knew for sure that I was going to make a mistake encoding the region, and the solver wasn't going to provide useful information abut what I did wrong. In cases like these, I like adding small tests and checks to catch mistakes early, because the solver certainly isn't going to catch them!
all_squares = set(product(range(size), repeat=2))
def test_i_set_up_problem_right():
assert all_squares == set(chain.from_iterable(regions.values()))
for r1, r2 in combinations(regions.values(), 2):
assert not set(r1) & set(r2), set(r1) & set(r2)
The first check was a quick test that I didn't leave any squares out, or accidentally put the same square in both regions. Converting the values into sets makes both checks a lot easier. Honestly I don't know why I didn't just use sets from the start, sets are great.
def render_regions():
colormap = ["purple", "red", "brown", "white", "green", "yellow", "orange", "blue", "pink"]
board = [[0 for _ in range(size)] for _ in range(size)]
for (row, col) in all_squares:
for color, region in regions.items():
if (row, col) in region:
board[row][col] = colormap.index(color)+1
for row in board:
print("".join(map(str, row)))
render_regions()
The second check is something that prints out the regions. It produces something like this:
111111111
112333999
122439999
124437799
124666779
124467799
122467899
122555889
112258899
I can compare this to the picture of the board to make sure I got it right. I guess a more advanced solution would be to print emoji squares like 🟥 instead.
Neither check is quality code but it's throwaway and it gets the job done so eh.
Update for the Internet
This was sent as a weekly newsletter, which is usually on topics like software history, formal methods, unusual technologies, and the theory of software engineering. You can subscribe here.
If you're reading this on the web, you can subscribe here. Updates are once a week. My main website is here.
My new book, Logic for Programmers, is now in early access! Get it here.